Irrotational Flow

Enough has been said about the subject of vorticity, its conservation and generation, that it should be obvious that an initially irrotational, uniform, inviscid flow will remain irrotational in the absence of heat transfer and of strong curved shocks. One important consequence of per­manent irrotationality is the existence of a velocity potential. That is, the equation

f = VxQ = 0 (1-55)

is a necessary and sufficient condition for the existence of a potential Ф such that

Q = V<f>, (1-56)

where Ф(х, у, г, t) or Ф(г, t) is the potential for the velocity in the entire flow. Its existence permits the replacement of a three-component vector by a single scalar as the principle dependent variable or unknown in theo­retical investigations.

Given the existence of Ф, we proceed to derive two important conse­quences, which will be used repeatedly throughout the work which follows.

1. The Bernoulli Equation for Irrotational Flow (Kelvin’s Equation).

This integral of the equations of fluid motion is derived by combining (1-3) and (1-28), and assuming a distant acting force potential:

DQ dQ IQ2′ Dt dt 2 у dt 2 у	l-Qxf	(1-57)
Under our present assumptions,
НЮ II S;|<s> &	„ /эф = VW’	(1-58)
so that (1-57) can be rearranged into
*[S+Ї+/	^ – ol = 0. p J	(1-59)

The vanishing of the gradient implies that, at most, the quantity involved will be a function of time throughout the entire field. Hence the least restricted form of this Bernoulli equation is

f + T + ly-11-™- <1Hi0)

In all generality, the undetermined time function here can be eliminated by replacing Ф with

Ф’ = Ф — jF(t) dt. (1-61)

This artificiality is usually unnecessary, however, because conditions are commonly known for all time at some reference point in the flow. For instance, suppose there is a uniform stream I7„ at remote points. There Ф will be constant and the pressure may be set equal to p„ and the force potential to SI» at some reference level.

F(t) = + j ~ — Q, * = const. (1-62)

The simplified version of (1-60) reads

ҐР

~ + m2 – Vl]+ ^ + [0. – Q] = 0. (1-63)

dt JPtx p

= V — P°° ip*>Ul 2 П~ 7-1 /дФ ~ УМ* IL1 al " dt

In isentropic flow with constant specific heat ratio 7, (1-63) is easily reorganized into a formula for the local pressure coefficient

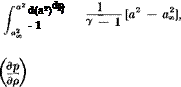Here a is the speed of sound and M = Ux/ax is Mach number. For certain other purposes, it is convenient to recognize that

(Note that, here and below, the particular form chosen for the barotropic relation is isentropic. Under this restriction, dp/dp, (dp/Sp),, and a2 all have the same meaning.)

This substitution in (1-63) provides a convenient means of computing the local value of a or of the absolute temperature T,

a2 – al = -(7 – 1) + i(Q2 – ul) + (Q. – Q)j • (1-67)

Finally, we remind the reader that the term containing the body-force potential is usually negligible in aeronautics.

2. The Partial Differential Equation for Ф. By substituting for p and Q in the equation of continuity, the differential equation satisfied by the velocity potential can be developed:

lf + V. Q_0. (Ь68)

The second term here is written directly in terms of Ф, as follows:

V ■ Q = V • (УФ) = V4,

і V2* =

which we identify as the familiar Laplacian operator,

To modify the first term of (1-68), take the form of Bernoulli’s equation appropriate to uniform conditions at infinity, for which, of course, a special case would be that of fluid at rest, U«, = 0. The body-force term is dropped for convenience, leaving

[ ~ ~ – UQ2 – ul). (1-70)

j Poo P 01

By the Leibnitz rule for differentiation of a definite integral,

d fP dp __ 1 dP h* P ~ P

We then apply the substantial derivative operator to (1-71) and make use of the first three members of (1-66),

ГР г – ГР ■

dp _ d I dp

Jpc p ~ Up Jp« p.

In view of (1-67) and of the simple relationship between the velocity vector and Ф, this is essentially the desired differential equation. If it is multiplied through by a2, one sees that it is of third degree in the unknown dependent variable and its derivatives. It reduces to an ordinary wave equation in a situation where the speed of sound does not vary signifi­cantly from its ambient values, and where the squares of the velocity components can be neglected by comparison with a2.

It is of interest that Garrick (1957) has pointed out that (1-74) can be reorganized into

v2*=Ml+о -v) (f+«• – v#) – h Ш *■ (i-re>

where the subscript conQc and on the substantial derivative is intended to indicate that this velocity is treated as a constant during the second application of the operators d/dt and (Q • V). Equation (1-75) is just a wave equation (with the propagation speed equal to the local value of a) when the process is observed relative to a coordinate system moving at the local fluid velocity Q.

The question of boundary conditions and the specialization of (1-74) and (1-75) for small-disturbance flows will be deferred to the point where the subject of linearized theory is first taken up.

1-8 The Acceleration Potential

It is of interest that when the equations of fluid motion can be simplified to the form

In a manner paralleling the treatment of irrotational flow, we can conclude that

a = V¥,

where ¥ (r, t) is a scalar function called the acceleration potential. Clearly,

¥ = П – ^ + G(t),

J P

G(t) being a function of time that is usually nonessential.

The acceleration potential becomes practically useful when disturbances are small, so that

In the absence of significant body forces, we then have

– V

poo

This differs only by a constant from the local pressure, and doublets of ¥ prove a very useful tool for representing lifting surfaces. The authors have not been able to construct a suitable partial differential equation for the acceleration potential in the general case, but it satisfies the same equation as the disturbance velocity potential in linearized theory.