KtjSSNER-SCHWARZ’ GENERAL SOLUTION
![]() By following the method of the previous sections, the aerodynamic force acting on a skeleton airfoil oscillating with arbitrary mode can be computed. Let the airfoil be located from x = — 1 to x — + 1 as in § 13.2, and let the harmonic oscillation of the points on the airfoil be described by
By following the method of the previous sections, the aerodynamic force acting on a skeleton airfoil oscillating with arbitrary mode can be computed. Let the airfoil be located from x = — 1 to x — + 1 as in § 13.2, and let the harmonic oscillation of the points on the airfoil be described by
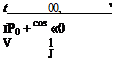 |
|
It is convenient to introduce a new variable x = cos 0* and consider v as a function of 0 and t. We can express v by a Fourier series:
UeiatP0= — I v(0,t)d6
7T JO
![]() UeM Pn = – і I v(6, t) cos и0 t/0
UeM Pn = – і I v(6, t) cos и0 t/0
7Г JO
With the upwash given in this form, the acceleration potential ф and the pressure distribution p can be determined as in the previous sections. The lift distribution can be written as
![]()
![]() /(0, I) = pU2emt ^2a0 tan~ + 4^Гая sin ndj
/(0, I) = pU2emt ^2a0 tan~ + 4^Гая sin ndj
Kiissner and Schwarz13-23 obtained the following relations: a0 = C(k)(P0 + jPj) — P
+ = ^ + Pn~Tn Pn+1 (n – ^
where C(k) is the Theodorsen’s function defined by Eq. 19 of § 13.4. (Kiissner writes (1 + T)j2 for C(k).)
|
2 [[36] – v(6, і TT Jo |
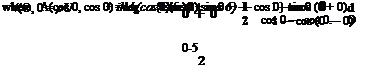 |
|
Using Eqs. 6, Kiissner and Schwarz derive the following general solution which is independent of the Fourier coefficients :f
The integral in Eq. 7 is defined by its Cauchy principal value. The total lift is then given by
L = J l • dx = J /(0, t) sin 0 d& (9)
and the moment about a point x0 — cos is
The result of integration gives the following expressions for the total lift and the stalling moment about the mid-point corresponding to the upwash given by Eq. 3:
![]() L = IrrpU^ [(/>„ + PL) C(k) + (P0 – P2) |
L = IrrpU^ [(/>„ + PL) C(k) + (P0 – P2) |
Aft/, = rrpU^ jP0 C(k) – PJ1 – C(k)] – (PL – P3) t – P* (12)
It is interesting to notice that the resultant lift depends on only the first three coefficients in Eq. 3, and the resultant moment on the first four. This is, in fact, connected with the general expression of the complex potential as given by Eq. 8 of § 13.3. It may be verified that the total lift depends only on the imaginary part of the coefficients A0 and A1, and the total moment depends only on the imaginary part of the coefficients A0 and A2.
Example. Lift Force Due to a Sinusoidal Gust. Let us consider the lift acting on an airfoil, flying at a uniform speed and entering a sinusoidal gust. If the coordinate axes are fixed on the airfoil, the vertical gust may be represented by a velocity distribution
w(x, t) = Weiw(t-xlL’] (13)
which expresses the fact that a sinusoidal gust pattern, with amplitude W (a constant), moves past the airfoil with the speed of flight U. If the wave length of the gust is /, the frequency со with which the waves pass any point of the airfoil is
со = lirUjl (14)
If the gust velocity w{x, t) is considered positive upward, the relative velocity at any point on the airfoil to the fluid (measured positive upward) is
v(x, t) = — Ц/е™1е-Цш! и)сов0 = _ ц/еішІе-ік cos в (15)
where the transformation x — cos в has been made for points on the
airfoil. Equation 15 may be put into the general form of Eq. 3 by the identity[37]
CO
eiz cos 0 = Ja(z) + 2 2* VB(z) cos nO (16)
n~l
where Jn{z)’s are Bessel functions of the first kind. Putting z = — к and noting that Jn(— z) = (~)nJn(z), it is seen that, according to Eqs. 15 and 16,
By comparing Eqs. 3 and 17, the expressions for the lift and moment can immediately be written according to Eqs. 11 and 12. If the chord length of the airfoil is c instead of 2, the lift and moment per unit span are
L = – npcUWe^ {[/0(£) – / /#)] C(k) -f – Шк) + J2(k)] 1} (18)
M1/a = Q рсЧіИ’е™1 {/„(A:) C(k) + пт – ОД]
+ [iUk) + iJ3(k)]~ + J2(k)] (19)
These expressions can be simplified by means of the recurrence formula for Bessel functions,
![]()
![]()
![]() 2 nJn(z)lz = Jn~i(z) + Jn+i(z) from which the following results are obtained:
2 nJn(z)lz = Jn~i(z) + Jn+i(z) from which the following results are obtained:
[J0(k)+J2(k)]j = iJL{k)
[iJL(k) + iJ3(k)]^= – .ОД
Therefore Eqs. 18 and 19 are reduced to
L = T! pcUWeitot ф(к) and
M4 = L–
h 4
where
ф(к) = [/„(*) – I Uk)]C{k) + / Aik) (23)
Clearly, the resultant lift acts through the ^-chord point from the leading edge. The factor тгрсІІф(к) represents the frequency response (admittance) of the lift to the gust. Writing
C(k) = F+iG (24)
where F, G are real functions of the reduced frequency k, we have
ф(к)* = (V + Л2)(Л + G2) + A2 + 2J0AG – 2J2F (25)
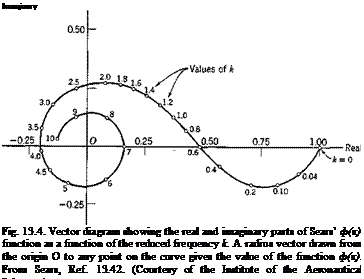 |
The function ф(к) is plotted as a vector diagram in Fig. 13.4. The function |^>(fc)|2 is plotted in Fig. 13.5. An approximate expression,
which agrees with the power-series expansion of Eq. 25 up to the first power in к and with the first term of the asymptotic expansion of Eq. 25 is
![]()
a A к
(a = 0.1811) (26)
Expression 26 approximates Eq. 25 closely over the whole range of к from 0 to oo. A simpler approximation is
![]()
![]() 1
1
1 + 2ттк
A comparison of Eqs. 25, 26, and 27 is given in Fig. 13.5. It is seen that Eq. 27 agrees fairly well with the exact expression 25, except for small values of k.
The solution 22 is due to Sears.13-42 The approximation 27 is due to Liepmann.911
|
Fig. 13.5. Comparison of approximate expressions of |#A)|!. |











