Mach Number Regimes

Of all the ways of subdividing and describing different aerodynamic flows, the dis­tinction based on the Mach number is probably the most prevalent. If M is the local Mach number at an arbitrary point in a flow field, then by definition the flow is locally:

Subsonic if M < I Sonic if M = 1 Supersonic if M > 1

Looking at the whole field simultaneously, four different speed regimes can be iden­tified using Mach number as the criterion:

1. Subsonic flow (M < 1 everywhere). A flow field is defined as subsonic if the Mach number is less than 1 at every point. Subsonic flows are characterized by smooth streamlines (no discontinuity in slope), as sketched in Figure 1.37a. Moreover, since the flow velocity is everywhere less than the speed of sound, disturbances in the flow (say, the sudden deflection of the trailing edge of the airfoil in Figure 1.37a) propagate both upstream and downstream, and are felt throughout the entire flow field. Note that a freestream Mach number M^ less than 1 does not guarantee a totally subsonic flow over the body. In expanding over an aerodynamic shape, the flow velocity increases above the freestream value, and if Moo is close enough to 1, the local Mach number may become supersonic in certain regions of the flow. This gives rise to a rule of thumb that Мж <0.8 for subsonic flow over slender bodies. For blunt bodies, Мж must be even lower to ensure totally subsonic flow. (Again, emphasis is made that the above is just a loose rule of thumb and should not be taken as a precise quantitative definition.) Also, we will show later that incompressible flow is a special limiting case of subsonic flow where M -> 0.

2. Transonic flow (mixed regions where M < landM > 1). As stated above, if

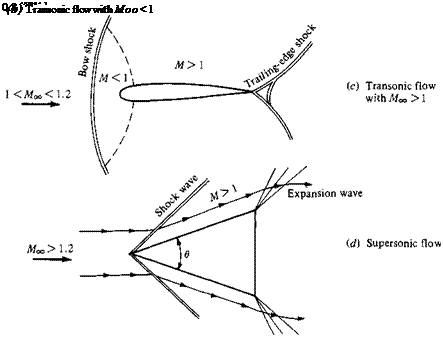
is subsonic but is near unity, the flow can become locally supersonic (M > 1). This is sketched in Figure 1.37b, which shows pockets of supersonic flow over both the top and bottom surfaces of the airfoil, terminated by weak shock waves behind which the flow becomes subsonic again. Moreover, if Mx is increased slightly above unity, a bow shock wave is formed in front of the body; behind this shock wave the flow is locally subsonic, as shown in Figure 1.37c. This subsonic flow subsequently expands to a low supersonic value over the airfoil. Weak shock waves are usually generated at the trailing edge, sometimes in a “fishtail” pattern as shown in Figure 1.37c. The flow fields shown in Figure 1.37b and c are characterized by mixed subsonic-supersonic flows and are dominated by the physics of both types of flow. Hence, such flow fields are called transonic flows. Again, as a rule of thumb for slender bodies, transonic flows occur for freestream Mach numbers in the range 0.8 < Мж < 1.2.

3. Supersonic flow (M > 1 everywhere). A flow field is defined as supersonic if the Mach number is greater than 1 at every point. Supersonic flows are frequently characterized by the presence of shock waves across which the flow properties

(a) Subsonic flow

Thin, hot shock layer with viscous interaction and chemical reactions

Moo> 5

(e) Hypersonic flow

Figure 1.37 Different regimes of flow.

and streamlines change discontinuously (in contrast to the smooth, continuous variations in subsonic flows). This is illustrated in Figure 1.37d for supersonic flow over a sharp-nosed wedge; the flow remains supersonic behind the oblique shock wave from the tip. Also shown are distinct expansion waves, which are common in supersonic flow. (Again, the listing of Мж > 1.2 is strictly a rule of thumb. For example, in Figure 131 d, if 9 is made large enough, the oblique shock

wave will detach from the tip of the wedge, and will form a strong, curved bow shock ahead of the wedge with a substantial region of subsonic flow behind the wave. Hence, the totally supersonic flow sketched in Figure .31d is destroyed if 9 is too large for a given M^. This shock detachment phenomenon can occur at any value of M^ > 1, but the value of в at which it occurs increases as Moo increases. In turn, if 9 is made infinitesimally small, the flow field in Figure l.31d holds for Moo > 1.0. These matters will be considered in detail in Chapter 9. However, the above discussion clearly shows that the listing of Moo > 1-2 in Figure 1.31 d is a very tenuous rule of thumb, and should not be taken literally.) In a supersonic flow, because the local flow velocity is greater than the speed of sound, disturbances created at some point in the flow cannot work their way upstream (in contrast to subsonic flow). This property is one of the most significant physical differences between subsonic and supersonic flows. Is is the basic reason why shock waves occur in supersonic flows, but do not occur in steady subsonic flow. We will come to appreciate this difference more fully in Chapters 7 to 14.

4. Hypersonic flow (very high supersonic speeds). Refer again to the wedge in Fig­ure .31d. Assume 9 is a given, fixed value. As Мж increases above 1, the shock wave moves closer to the body surface. Also, the strength of the shock wave in­creases, leading to higher temperatures in the region between the shock and the body (the shock layer). If Мх is sufficiently large, the shock layer becomes very thin, and interactions between the shock wave and the viscous boundary layer on the surface occur. Also, the shock layer temperature becomes high enough that chemical reactions occur in the air. The O2 and N2 molecules are torn apart; i. e., the gas molecules dissociate. When Мх becomes large enough such that viscous interaction and/or chemically reacting effects begin to dominate the flow (Figure 1.37e), the flow field is called hypersonic. (Again, a somewhat arbitrary but frequently used rule of thumb for hypersonic flow is Мж > 5.) Hypersonic aerodynamics received a great deal of attention during the period 1955-1970 because atmospheric entry vehicles encounter the atmosphere at Mach numbers between 25 (ICBMs) and 36 (the Apollo lunar return vehicle). Again during the period 1985-1995, hypersonic flight received a great deal of attention with the concept of air-breathing supersonic – combustion ramjet-powered transatmo­spheric vehicles to provide single-stage-to-orbit capability. Today, hypersonic aerodynamics is just part of the whole spectrum of realistic flight speeds. Some basic elements of hypersonic flow are treated in Chapter 14.

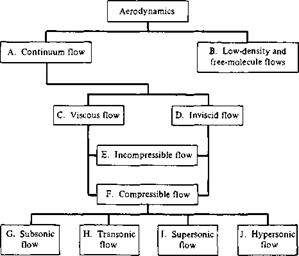
In summary, we attempt to organize our study of aerodynamic flows according to one or more of the various categories discussed in this section. The block diagram in Figure 1.38 is presented to help emphasize these categories and to show how they are related. Indeed, Figure 1.38 serves as a road map for this entire book. All the material to be covered in subsequent chapters fits into these blocks, which are lettered for easy reference. For example, Chapter 2 contains discussions of some fundamental aerodynamic principles and equations which fit into both blocks C and D. Chapters 3 to 6 fit into blocks D and E, Chapter 7 fits into blocks D and F, etc. As we proceed

Figure 1.38 Block diagram categorizing the types of aerodynamic flows.

with our development of aerodynamics, we will frequently refer to Figure 1.38 in order to help put specific, detailed material in proper perspective relative to the whole of aerodynamics.