Simplifications and Explications
It is not surprising that the mathematical complexity of the inertial coupling problem and the relatively crude state of early analog and digital computers led researchers and designers to try to capture the essence of the problem with simplified mathematical models. With current computer technology, most engineering groups faced with such a problem would probably run the problem without simplification, but automate it so as to use a minimum amount of engineering time.
A strategy made possible by modern digital computers would be to step through automatically all combinations of rolling velocity, Mach number, altitude, center of gravity, initial load factor, stability augmentation feedback, and control usage. This would generate vast numbers of 5- or 6-degree-of-freedom transients. While still in computer memory, the transients could be screened by algorithms that look for excessive air loads or divergences. Only the interesting cases would be retrieved for engineering examination.
|
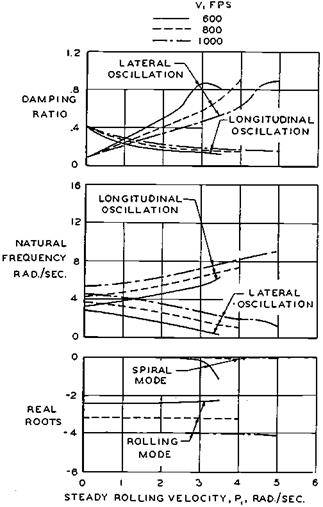
Figure 8.6 Effect of steady rolling on small-perturbation modes of motion of the Douglas F4D-1. Damping of the longitudinal short-period oscillation is halved at high roll rates. (From Abzug, Jour. of the Aero. Sciences, Nov. 1954) |
However, back in the late 1940sand 1950s, ingenioussimplificationswere the order of the day rather than the modern head-on approach hypothesized above. Leading the simplification parade in the early days was W. H. Phillips’ original work, in which he squeezed the inertial coupling problem down to the solution of a simple quadratic equation. Six of the engineers who came shortly afterward tried to improve on the simplified Phillips model.
An early approach linearized the full 6-degree-of-freedom equations of motion under conditions of steady rolling (Abzug, 1954). Calculations for the F4D Skyray showed a reduction in damping and increase in frequency of the longitudinal oscillation as roll rate increased beyond about 150 degrees per second (Figure 8.6). The succeeding simplified approaches are documented in the proceedings of the Wright Field Inertial Coupling Conference (Westbrook, 1956).
Robert Bratt and Charles DaRos reduced the inertial coupling problem to the solution of a quartic, whose roots they determined as functions of rolling velocity. This required setting lateral acceleration to zero and rolling velocity and normal acceleration to constants. Very interesting by-products of the Bratt-DaRos approach were steady-state solutions for angles of sideslip and attack under rolling conditions.
Cecil Carter returned to the Phillips model, but added two additional degrees of freedom, translation along the lateral (Y) and normal (Z) axes. Carter found stability boundaries from the resultant fourth-degree characteristic equation by Routh’s criterion, a fairly standard procedure. Unfortunately, in checking the stability boundary results against 20 actual roll time histories, only fair agreement was found, and Carter concluded that the modified Phillips method needed to be supplemented by more exact calculations.
Like Bratt and DaRos, Schmidt, Bergrun, and Merrick reasoned that the steady-state angles of attack and sideslip reached in steady roll would be useful indices of the severity of any unwanted excursions. Their method, partly based on a more limited study by Uddenberg at Boeing, used the full 5-degree-of-freedom (airspeed constant) equations of motion with only very minor simplifications. Very interesting correlations appeared with not only Phillips’ work, but also with complete simulations and a flight test point for the North American F-100A. The Schmidt, Bergrun, and Merrick analysis predicted quite accurately the gains obtained with a larger vertical tail on the F-100A.
Kelley at Grumman started with the Abzug equations for steady rolling, eliminating the cyclic gravity terms and other small terms and implicitly incorporating F-11F stability derivatives. A preliminary linear algebraic solution, including some trial and error because of the dependence of stability derivatives on the answers, found steady-state values of pitching velocity and angles of attack and sideslip corresponding to some steady rolling velocity. A final perturbation solution from the steady-state values was found from fifth-order linear differential equations. Kelley limited this to just the roots, determining stability.
The sixth post-Phillips venture in inertial coupling simplification was that by Gautraud and Flanders at MIT. They too linearized the problem around a presumed steady rolling condition, but adopted a more controls-oriented approach, finding both poles and zeros for the Convair F-102.
Augmenting the inertial coupling simplification studies was the work done to explain the phenomenon and to pick it apart for specific cases. What factors are really important? John Wykes dissected the F-100 yawing and sideslip acceleration time histories, showing the relative importance of aerodynamic, engine gyroscopic, and inertial terms as the roll proceeded (Figure 8.7)
Engine angular momentum enters into the inertial coupling problem as a bias in one direction of roll. Divergence occurs at a slightly lower roll rate when rolling in a sense opposite to engine rotation (Pinsker, 1957). Propeller and engine gyroscopic effects occur as well in other flight regimes, especially when aerodynamic forces and moments are relatively low, such as in spins and in takeoff.