Singular Perturbatio Problems

3- 1 Introduction

The treatment given in the preceding chapter is of fairly limited practical use for engineering problems. Constant-density inviscid and irrotational flow is there rather considered as a physical model for subsonic flows in general from which interesting qualitative information can be extracted but not always accurate quantitative results. Thus, despite d’Alembert’s paradox, the drag in a two-dimensional flow is certainly not zero, but the proper interpretation of the theoretical result is that, in a steady (attached) flow, drag forces are generally much smaller than either lift or forces due to unsteady motion. The practical conclusion one can draw from the inviscid model is that flow separation should be avoided at all costs. This calls for rather blunt-nosed shapes with no abrupt slope or curvature changes or protuberances, and with gently sloping rear portions, i. e., “streamlined ” bodies.

Apart from the drag which is dominated by viscosity—the very thing that was neglected in the simplified model—the constant-density theory is able, in many practical cases, to produce remarkably good approxima­tions to pressure distributions for speeds less than, say, half the speed of sound. Unfortunately, the calculation of inviscid flow for shapes of en­gineering interest is usually so difficult that one is forced to make some further approximation in order to obtain a result. For all the simple shapes considered in Chapter 2 (with the exception of certain airfoils and the ellipsoids with large fineness ratio) the nonviscous solutions happen to be almost completely useless, since in reality the flow will separate and the simplified model then loses its validity. The example emphasizes the fact that extreme caution must be exercised when using the physical model to obtain approximate engineering results rather than just to gain a general qualitative understanding of the physical situation and the mathematical structure of the problem. Considerable insight is generally required to judge when a simplified model will provide a useful first approximation to an actual physical situation.

The discussion may suffice to emphasize the basic difference between physical models and approximate solutions; for the former, one seeks an exact solution to a simplified and very often an artificial problem whereas,

loosely speaking, in the latter, one seeks a simplified solution to a real problem. The distinction should always be kept in mind although it is not always clear-cut. For example, the continuum model of gas is also a very good approximation for all the problems that we will consider.

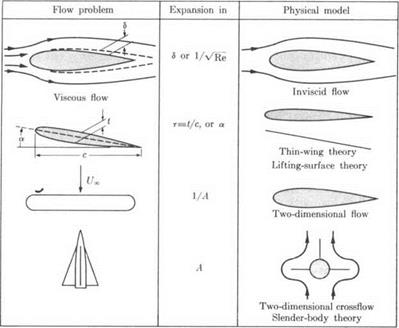
There are a variety of methods to obtain useful approximations. We shall discuss two different methods which are the ones mostly used in aerodynamic problems. One is the expansion in powers of a small parameter. Often the first term in this expansion may by itself be con­sidered as a physical model. Some of the expansions that will be discussed and the physical models derived in this manner are illustrated in Fig. 3-1.

A great majority of problems in fluid mechanics have been successfully attacked by series-expansion methods. The series obtained are usually only semiconvergent, i. e., asymptotic, and also frequently not uniformly valid. These features, which are closely associated with the so-called singu­lar perturbation nature of such problems, will be thoroughly discussed in the following section.

The second method of approximation that will be considered is the purely numerical one. In the future this will undoubtedly become of increasing importance as the full potentialities of modem computing devices are realized among aerodynamicists. There are many difficulties associated with numerical solutions. First of all, the equations for fluid flow are so complicated that no one has as yet succeeded in a step-by-step integra­tion of the full gas dynamic equations even assuming a perfect, inviscid gas. Therefore, the examples given will concern the numerical solution of linearized problems. Second, it is very hard to estimate the error induced by the approximation scheme employed. In contrast, this could in principle always be done in the analytical series solution by estimating the first neglected term. For this purpose, and for checking out the computational program, the analytical solutions for the limiting cases are extremely useful. Thus, far from making them obsolete, the new possi­bilities for numerical solutions give the analytical solutions extended practical usefulness.