Slender-Body Theory
5- 1 Introduction
We shall now study the flow around configurations that are “slender” in the sense that all their crosswise dimensions like span and thickness are small compared to the length. Such a configuration could, for example, be a body of revolution, a low-aspect ratio wing, or a low-aspect ratio wing-body combination. The formal derivation of the theory may be thought of as a generalization to three dimensions of the thin airfoil theory; however, the change in the structure of the inner solution associated with the additional dimension introduces certain new features into the problem with important consequences for the physical picture.
The simplest case of a nonlifting body of revolution will be considered first in Sections 6-2 through 6-4 and bodies of general shape in Sections 6-5 through 6-7.
6- 2 Expansion Procedure for Axisymmetric Flow
We shall consider the flow around a slender nonlifting body of revolution defined by
r = R{ x) = eR(x) (6-1)
for small-values of the thickness ratio e. For steady axisymmetric flow the differential equation (1-74) for Ф reads
2
(a2 – Ф2)ФХХ + (a2 – Ф?)ФГГ + у Фг – 2ФХФГФХГ = 0, (6-2)
where
a2 = a2 – (ФI + Фг2 – Ul). (6-3)
The requirement that the flow be tangent to the body surface gives the following boundary condition:
~ _ e dR r _ ед (6-4)
Фх ах
We shall consider an outer expansion of the form
![]() Ф° = f7„[z + бФЇ(ж, r) – f е2Ф2(ж, г) + ■ • • ]
Ф° = f7„[z + бФЇ(ж, r) – f е2Ф2(ж, г) + ■ • • ]
99
and an inner expansion
Ф* = UK[x + еФ(х, f) + е2Фl(x, ?) + •■•], (6-6)
where
f = r/e. (6-7)
As in the thin airfoil case Ф) must be a function of x, only, because otherwise the radial velocity component
U, = Ф* = £/„[ФІг + еФг? + • • • ] (6-8)
will not vanish in the limiting case of zero body thickness. Substituting (6-6) into (6-2) and (6-3) and retaining only terms of order e°, we obtain
Фггг + г Фгг = 0. (6-9)
r
![]() The solution of (6-9) satisfying (6-10) is easily shown to be ФІ = EE’In г + Ых),
The solution of (6-9) satisfying (6-10) is easily shown to be ФІ = EE’In г + Ых),
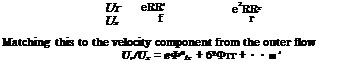 |
|
in which the function t/2 must be found by matching to the outer flow. From (6-11) it follows that the radial velocity component is
we find that Ф°г must be zero as r —» 0. The only solution for Ф° that will, in addition, satisfy the condition of vanishing perturbations at infinity, is a constant which is taken to be zero. The perturbation velocities in the outer flow are thus of order e2 as compared to e in both the twodimensional and finite-wing cases. That the flow perturbations are an order of magnitude smaller for a body of revolution is reasonable from a physical point of view since the flow has one more dimension in which to get around the body.
Since Ф° = 0 it follows by matching that also Ф) = 0. This will have the consequence that all higher-order terms of odd powers in e will be zero, and the series expansion thus proceeds in powers of e2. With Ф? = 0, substitution of the series for the outer flow into (6-2) and (6-3) gives
for the lowest-order term
(1 – M2)Ф°2хх + ~ ФІг + Фirr = 0. (6-14)
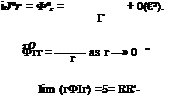 |
||
The matching of the radial velocity component requires according to (6-12) that in the limit of r —> 0
The boundary condition at infinity is that Ф£х and Ф£, vanish there. Matching of Ф2 itself with Ф2 as given by (6-11) yields
<?2(ж) = lim [Ф2 — RR’ In r] + RR’ In e. (6-17)
r—>0
The last term comes from the replacement of f by r/e in (6-11). It follows that the inner solution is actually of order e2 In e rather than e2 as was assumed in the derivation. However, from a practical point of view, we may regard In e as being of order unity since In e is less singular in the limit of € —> 0 than any negative fractional power of e, however small.
In calculating the pressure in the inner flow it is necessary to retain some terms beyond those required in the thin-airfoil case. By expanding (1-64) for small flow disturbances we find that
which, upon introduction of the inner expansion, gives
Cp = —є2[2Ф2і + (Фгг)2] + • • • (6-19)
The terms neglected in (6-19) are of order e4 In e, or higher.
As was done in the case of a thin wing, we introduce a perturbation velocity potential <p, in the present case defined as
![]() <P = е2Фг.
<P = е2Фг.
The equations derived above then become for the outer flow
where S(x) = ttR2(x) is the cross-sectional area of the body. The pressure near the body surface is given by
CP = —(2<px + *?) (6-23)
to be evaluated at the actual position r (for r = 0 it becomes singular). From the result of the inner expansion it follows that in the region close to the body
<P ^ ^ S'(x) In r + g{x), (6-24)
where g(x) is related to <Ь(я) in an obvious manner.
In (6-24), the first term represents the effect of local flow divergence in the crossflow plane due to the rate of change of body cross-sectional area. According to the slender-body theory this effect is thus seen to be approximately that of a source in a two-dimensional constant-density flow in the – y, z-plane. Hence, the total radial mass outflow in the inner region is independent of the radius r, as is indeed implied in the boundary condition (6-22). The second term, g(x), contains the Mach number dependence and accounts for the cumulative effects of distant sources in a manner that will be further discussed in the next section.











