The Kutta Condition and Lift

As is familiar to every student of aerodynamics, Joukowsky and Kutta discovered independently the need for circulation to render the two­dimensional, constant-density flow around a figure with a pointed trailing edge physically reasonable. This is a simple example of a scheme for fixing the otherwise indeterminate circulation around an irreducible path in a doubly connected region. It is one of a number of ways in which viscosity can be introduced at least indirectly into aerodynamic theory without actually solving the equations of Navier and Stokes. The circulation gives rise to a lift, which is connected with the continually increasing Kelvin impulse of the vortex pair, one of the vortices being the circulation bound to the airfoil, while the other is the “starting vortex ” that was generated at the instant the motion began.

With respect to the lifting airfoil, we reproduce a few important results from Sections 7.40-7.53 of Milne-Thompson (1960). Let the profile and the circle which is being transformed into it be related as shown in Fig. 2-17.

It is assumed that the transformation

£=f + ^ + p + — -> (2-156)

which takes the circle into the airfoil, is known. It can be proved that the resulting force is normal to the oncoming stream and equal to

L = pt/„r. (2-157)

Here Г is the circulation bound to the airfoil, which incidentally may or may not satisfy the full Kutta condition of smooth flow off from the trailing edge. If this condition is entirely met, which is equivalent to neglecting the effect of displacement thickness of the boundary layer and’ the wake thickness at the trailing edge, then the circulation is given by

Г = ітгі/^а sin <*z. l.- (2-158)

All the quantities here are defined in the figure. In particular, az. L. is the angle of attack between the actual stream direction and the zero-lift (Z. L.) direction, determined as a line parallel to one between the center of the circle in the f-plane and the point Hi which transforms into the airfoil trailing edge. Combining (2-157) and (2-158), we compute the lift

L = 4wpl7^a sin «z. l.- (2-159)

From this we find that the lift-curve slope, according to the standard aeronautical definition, is slightly in excess of 2ir, reducing precisely to 2ж when the airfoil becomes a flat plate of zero thickness, i. e., when the radius a of the circle becomes equal to a quarter of the chord.

The airfoil is found to possess an aerodynamic center (A. C.), a moment axis about which the pitching moment is independent of angle of attack. This point is located on the Z-plane as shown in Figs. 7.52 and 7.53 of Milne-Thompson (1960). The moment about the aerodynamic center is

MA. C. = — 2жрІІ212 sin 27, (2-160)

where

ai = (le~iy)2. (2-161)

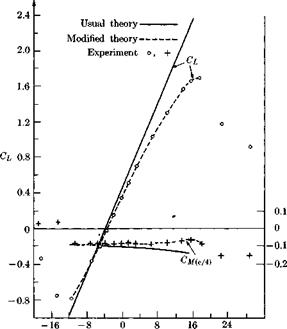
Figure 2-18 gives some indication of the accuracy with which lift and moment can be predicted. The theoretical value of zero for drag in two dimensions is the most prominent failure of inviscid flow methods. It represents a nearly achievable ideal, however, as evidenced by the lift-to – drag ratio of almost 300 from a carefully arranged experiment, which is reported on page 8 of Jones and Cohen (1960).

Fig. 2-18. Comparisons between predicted and measured lift coefficients and quarter-chord moment coefficients for an NACA 4412 airfoil. “Usual theory” refers to Theodorsen’s procedure, whereas the modifications involve changing the function е(ф) so as to make circulation agree with the measured lift at a given angle of attack. [Adapted from Fig. 9 of Pinkerton (1936).]

More information will be found in Chapter 4 of Thwaites (1960) on refined ways of calculating constant-density flow around two-dimensional airfoils. In particular, these include reference to a modern theory by Spence and others which makes allowance for the boundary layer thickness and thus is able to carry the calculation of loading up to much higher angles of attack, even approaching the stall.