Theoretical Studies

The carrier-approach problem for naval aircraft received a great deal of atten­tion from leading aeronautical research organizations, starting in the late 1950s. We note

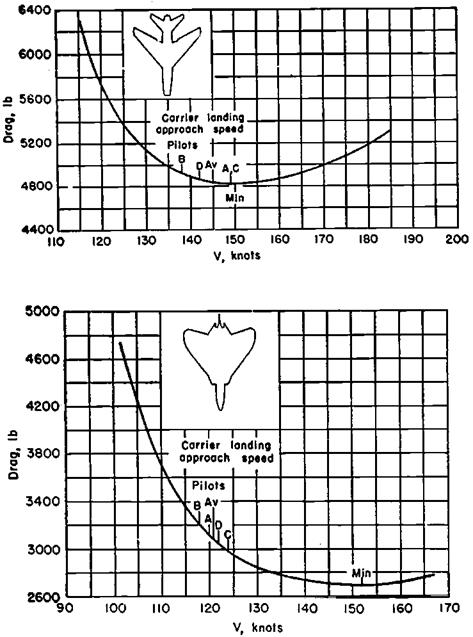
Figure 12.2 Carrier landing approach airspeeds chosen by pilots are below the airspeed for minimum drag forboththeNorthAmericanF-100A (top) andthe Douglas F4D-1 (bottom). (FromWhite, Schlaff, and Drinkwater, NACA RM A57L11, 1957)

particularly contributions to the theory by groups at the NACA Ames Aeronautical Labora­tory, the Royal Aeronautical Establishment, and Systems Technology, Inc. Two main lines of investigation were prediction of the minimum acceptable carrier-approach airspeed for any airplane and the physics of optimum vertical path control during approaches.

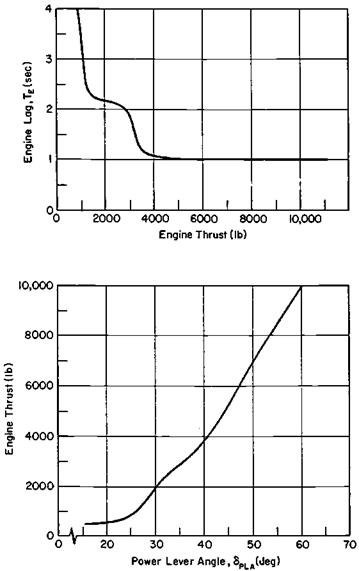
Figure 12.3 Ling-Temco-Vought A-7E engine response characteristics. Lag in developing engine thrust is large at low power settings, creating path control problems in carrier approach. (From Craig, Ringland, and Ashkenas, Syst. Tech., Inc. Rept. 197-1, 1971)

The NACA Ames group examined some five candidate predictors for minimum ap­proach airspeeds (Drinkwater and Cooper, 1958). As found earlier, minimum drag speed correlated poorly with minimum acceptable carrier-approach airspeed. Other performance – related criteria were no better. Two that failed to correlate were the minimum air­speeds at which a given rate of change of flight path angle or a 50-foot climb could be obtained.

In the end, the Ames researchers concluded that a simple criterion based on stalling speed correlated best with the data. The minimum comfortable carrier-approach airspeed agreed best with 115 percent of the stalling speed in the power approach (PA) configuration, that is, flaps and landing gear down, power for level flight.

The Ames result is valid for airplanes of the general type tested, but one might be concerned at applying the 115-percent stalling speed prediction result to airplanes that differ radically from those tested. It seemed logical to try to develop a carrier-approach flight path model based on the fundamental flight and control dynamics and human factors of the problem. That was the motivation behind the work at Systems Technology, Inc., sponsored by the U. S. Navy. The STI engineers, including Tulvio S. Durand, Irving L. Ashkenas, Robert F. Ringland, C. H. Cromwell, Samuel J. Craig, Richard J. Wasiko, and Gary L. Teper, brought to the carrier-approach problem their well-known systems analysis techniques.

An interesting result, due to Ashkenas and Durand, identifies the transfer function pa­rameter associated with minimum drag speed, the point at which height control by elevator becomes reversed from the normal sense. This is a numerator factor in the elevator to height transfer function called 1/Th1. Negative values of this factor put a zero in the right half of the s-plane. Closing the height to elevator loop results in an aperiodic divergence corresponding to the reversal of normal height control below the minimum drag speed.

Around 1962, Ashkenas came up with the first systems analysis basis for minimum carrier-approach airspeed prediction. That is, his prediction for minimum approach airspeed was based on assumed pilot loop closures with an airframe defined by arbitrary mass, aerodynamic, and thrust characteristics (Ashkenas and Durand, 1963). Since the systems analysis approach does not merely correlate the behavior of existing airplanes, the results should apply to airplanes not yet built whose characteristics are beyond the range of those tested so far.

The Ashkenas-Durand systems analysis prediction for minimum carrier approach air­speeds can be explained as follows:

1. The approach is assumed to be made in gusty air.

2. In gusty air the pilot attempts to close the pitch attitude loop at a higher frequency than the gust bandwidth, or as high a frequency as possible.

3. The highest possible pitch attitude loop bandwidth occurs when the pilot’s gain is so high that the closed-loop system is just neutrally stable.

4. By excluding pilot model leads and lags, or treating the pilot as a pure gain, a definite gain value is associated with the neutrally stable closed pitch loop.

5. Similarly, an outer altitude control loop is closed by the pilot using pure gain, or thrust proportional to altitude error.

6. With both pitch and altitude control loops closed by the pilot, the sensitivity of the pitch control loop break frequency to pilot pitch control gain is calculated, as a partial derivative.

7. The sign of this partial derivative of pitch loop bandwidth to pilot pitch control gain, called the reversal parameter, is taken as an indication of carrier-approach performance. Positive reversal parameter values mean that increasing pilot gain improves bandwidth and performance.

8. The lowest airspeed at which the reversal parameter is positive is taken as a pre­diction of minimum carrier-approach airspeed.

The reversal parameter was refined in subsequent studies by Ashkenas and Durand in 1963 and by Wasicko in 1966. An interesting consideration was the finding in 1964 by Durand and Teper that the carrier-approach piloting technique as the airplane nears the carrier ramp changes from that assumed in the reversal parameter model. However, the approach airspeed would have already been set in the early part of the approach.

A later (1967) study of the carrier-approach problem by Durand and Wasicko went into the problem in greater detail, including the dynamics of the optical projection device that pilots use as a glide slope beam. The 1 /Te2 zero in the pitch attitude to elevator transfer function turned up as a primary factor, both in simulation and in landing accident rates. Unfortunately, this zero is dominated by airplane lift curve slope and airplane wing loading. Lift curve slope in turn is fixed by wing aspect ratio and sweep.

Wing loading, aspect ratio, and sweep are among the most fundamental of all design parameters for an airplane, affecting its flight performance. When a new carrier-based airplane is being laid out and wing loading, aspect ratio, and sweep are being selected to maximize such vital factors as range and flight speed, it is hard to imagine that a statistical connection with landing accident rate will be prominent in the trade-off.

Systems analysis methods were applied again to the carrier-approach problem in 1990 by Robert K. Heffley of Los Altos, California. Heffley studied the factors that control the carrier-approach outer loop involving flight path angle and airspeed. The higher-frequency pitch attitude inner loop was suppressed in the analysis, assumed to be tightly regulated by the pilot.

Heffley closed the outer loop under three different strategies, depending on whether the airplane was on the front side or back side of the drag required curve. The results give interesting insights into factors affecting the approach (Heffley, 1990). Another study in this series is an application of the Hess Structural Pilot Model (discussed in Chapter 21) to the carrier-approach problem, using a highly simplified pilot-airframe dynamic model.

The current U. S. Navy criterion for minimum carrier-approach speed, as exemplified by the system specification for the F/A-18 Hornet, gives no fewer than six possible limiting airspeeds, such as the lowest speed at which a 5-foot per second squared longitudinal acceleration can be attained 2.5 seconds after throttle movement and speed brake retraction. Heffley concludes that two additional criteria might be needed. One is a refinement of existing lag metrics to one that combines coordinated pitch attitude and thrust inputs. The other is an extension of the popup maneuver dealing with the end game, when the airplane is quite near the carrier’s ramp.