Thin-wing Theory

4- 1 Introduction

In this chapter we shall derive the equations of motion governing the sub – or supersonic flow around thin wings. Although this problem may be handled by simpler regular perturbation methods, we shall here instead use the method of matched asymptotic expansions for basically two reasons. First, the present method gives a clearer picture of the usual linearized formulation as that for an outer flow for which the wing in the limit collapses onto a plane (taken to be z = 0). Secondly, the similarities and dissimilarities between the airfoil problem and that for a slender body of revolution, which will be treated in the following chapter, will be more readily apparent; in fact, as will later be seen, the slender-body theory formulation can be obtained from the two-dimensional airfoil case by means of a simple modification of the inner solution.

The procedure will be carried out in detail for two-dimensional flow only, but the extension to three dimensions is quite straightforward. The first term in the series expansion leads to the well-known linearized wing theory. In this chapter, the solutions for two-dimensional flow are given as examples. Three-dimensional wings will be considered in later chapters. The case of transonic flow requires special treatment and will be deferred to Chapter 12.

4- 2 Expansion Procedure for the Equations of Motion

Anticipating the three-dimensional wing case, for which the standard choice is to orient the wing in the x, y-plane, we shall this time consider two-dimensional flow in the x, «-plane around a thin airfoil located mainly along the ж-axis with the free stream of velocity [/„ in the direction of the positive ж-axis as before. Thus, referring to Fig. 5-1, we let the location of the upper and lower airfoil surfaces be given by

zu = tfu(x) = тд(х) + вЦх) — ax zi = ifi(x) = —тд(х) + вЛ{ x) — ax,

where e is a small dimensionless quantity measuring the maximum cross­wise extension of the airfoil, r its thickness ratio, a the angle of attack, and 0 is a measure of the amount of camber. The functions g(x) and h(x)

81

define the distribution of thickness and camber, respectively, along the chord. It will be assumed that g and h are both smooth and that g’ and h1 are of order of unity everywhere along the chord. A blunt leading edge is thus excluded. In the limit of e —» 0 the airfoil collapses to a segment along the z-axis assumed to be located between x = 0 and x = c. We will seek the leading terms in a series expansion in e of Ф to be used as an approximation for thin airfoils with small camber and angle of attack.

For two-dimensional steady flow the differential equation (1-74) for Ф simplifies to

(a2 – Ф2Х)ФХХ + (a2 – Ф2)Фгг – 2ФхФгФхг = 0, (5-2)

where the velocity of sound is given by (1-67), which, for the present case, simplifies to

a2 = a2 – {Ф2Х + Ф2 – Vl). (5-3)

From Ф the pressure can be obtained using (1-64):

1 •——– ^ (ф| + ф l-Ul) – 1 ■ (5-4)

2 al J )

The boundary conditions are that the flow is undisturbed at infinity and tangential to the airfoil surface. Hence

Фг/Фх = 6 0П г = «/u Фг/Фх = on z=eji.

Additional boundary conditions required to make the solution unique for a subsonic flow are that the pressure is continuous at the trailing edge (Kutta-Joukowsky condition) and also everywhere outside the airfoil. In a supersonic flow, pressure discontinuities must satisfy the Rankine – Hugoniot shock conditions. However, to the approximation considered here, these are always automatically satisfied. Strictly speaking, a super­

sonic flow with curved shocks is nonisentropic, and hence nonpotential, but the effects of entropy variation will not be felt to within the approxi­mation considered here, provided the Mach number is moderate.

We seek first an outer expansion of the form

Ф° = Г/„[Фо(ж, z) + €Ф?0, z) + • • •]. (5-6)

The factor U„ is included for convenience; in this manner the first partial derivatives of the Фп-terms will be nondimensional. Since the airfoil in the limit of € —> 0 collapses to a line parallel to the free stream, the zeroth – order term must represent parallel undisturbed flow. Thus

Ф°о = x. (5-7)

By introducing the series (5-6) into (5-2) and (5-3), and using (5-7), we obtain after equating terms of order e

(1 – М2)Ф°1хх-+ Ф?« = 0. (5-8)

The only boundary condition available for this so far is that flow perturba­tions must vanish at large distances,

і Фіг —» 0 for sjx2 + г2

The remaining boundary conditions belong to the inner region and are to be obtained by matching. The inner solution is sought in the form

£/„[Фо(ж, z) + еФі(а;, z) + б2Ф’2(х, «) + •••], (5-10)

z = г/t. (5-11)

This stretching enables us to study the flow in the immediate neighborhood of the airfoil in the limit of e —> 0 since the airflow shape then remains independent of € (see Fig. 5-2) and the width of the inner region becomes of order unity. The zeroth-order inner term is that of a parallel flow, that is, Фо = x, because the inner flow as well as the outer flow must be parallel in the limit t —> 0.

(This could of course also be obtained from the matching procedure.) From the expression for the IF-component,

Фг = – еФІ = Ux[$Ux, z)

«ФггОг, г) +

we see directly that Ф} must be independent of z, say Ф = (ji(x) (which in general is different above and below the airfoil), otherwise W would not vanish in the limit of zero e. Hence (5-10) may directly be simplified to

Ф1 = U<t,[x + — є2Ф2(ж, z) + • • • ]. (5—13)

By substituting (5-13) into the differential equation (5-2) and the asso­ciated boundary condition (5-5) we find that

Фк* = 0, (5-14)

Фг = for г = Ju(x)

(5-15)

Фіі = for z = Ji(x).

Thus, the solution must be linear in z,

ФІ = Ї§+Мї), (5-16)

for z >7u, with a similar expression for 2 < fi. This result means that to lowest order the streamlines are parallel to the airfoil surface throughout the inner region.

The inner solution cannot, of course, give vanishing disturbances at infinity since this boundary condition belongs to the outer region. We

therefore need to match the inner and outer solutions. This can be done in two ways; either one can use the limit matching principle for W or the asymptotic matching principle for Ф. From (5-16) it follows that W’ is independent of z to lowest order, hence in the outer limit 2 = oo

Wi0 = Ut(x, oo) = e^“- (5-17)

Now

W° = еФ°1г. (5-18)

Equating the inner limit (z = 0+) to (5-17), we obtain the following boundary condition:

*u(x, 0+)=J> (5-19)

and in a similar manner

Фї.(*,0-) =§• (5-20)

By matching the potential itself we find that

Viu(x) = Фї(*,0+). (5-21)

To determine it is necessary to go to a higher order in the outer solution.

To illustrate the use of the asymptotic matching principle we first express the two-term outer flow in inner variables,

Ф° = TJ*[x + ez) + • • • ], (5-22)

and then take the three-term inner expansion of this, namely

Ф0 = U„[x + еФ°г(х, 0+) + е2гФ°1г(х, 0+) + • ■ • ], (5-23)

which, upon reexpression in outer variables yields

Ф0 = U*[z + еФІ(х, 0+) + егФЇЛх, 0+) + • • • ]■ (5-24)

The three-term inner expansion, expressed in outer variables, reads

dju

with the three-term inner expansion of the two-term outer expansion as given by (5-23) leads to

as before.

From the velocity components we may calculate the pressure coefficient by use of (5-4). Expanding in e and using (5-21) we find that the pressure on the airfoil surface is given by

Cp = ~2еФ°1х(х, 0±), (5-27)

where the plus sign is to be used for the upper surface and the minus sign for the lower one.

An examination of the expression (5-25) makes clear that such a simple inner solution cannot hold in regions where the flow changes rapidly in the x-direction as near the wing edges, or near discontinuities in airfoil surface slope. For a complete analysis of the entire flow field, these must be considered as separate inner flow regions to be matched locally to the outer flow. The singularities in the outer flow that are usually encountered at, for example, wing leading edges, do not occur in the real flow and should be interpreted rather as showing in what manner the perturbations due to the edge die off at large distances. For a discussion of edge effects on the basis of matched asymptotic expansions, see Van Dyke (1964).

In the following we will use the notation

6ФЇ = <p,

where <p is commonly known as the velocity perturbation potential (the factor Ux is sometimes included in the definition). The above procedure is easily extended to three dimensions, and for ip we then obtain the follow­ing set of linearized equations of motion and boundary conditions:

where S is the part of the x, у-plane onto which the wing collapses as e —> 0.

Fig. 5-3. Separation of thickness and lift problems.

Since the equations of motion and the boundary conditions are linear, solutions may be superimposed linearly. It is therefore convenient to write the solution as a sum of two terms, one giving the flow due to thickness and the other the flow due to camber and angle of attack (see Fig. 5-3). Thus we set

where

on S. It follows from (5-33) and (5-34) that <p‘ is symmetric in z whereas <pl is antisymmetric. As indicated in Fig. 5-3, represents the flow around a symmetric airfoil at zero angle of attack whereas <pl represents that around an inclined surface of zero thickness, a “lifting surface.” It will be apparent from the simple examples to be considered below that the lifting problem is far more difficult to solve than the thickness problem, at least for subsonic flow.

Another consequence of the lineariza­tion of the problem is that complicated solutions can be built up by superposition of elementary singular solutions. The ones most useful for constructing solu­tions to wing problems are those for a source, doublet and elementary horseshoe vortex. For incompressible flow the first two have already been discussed in Chap­ter 2. The elementary horseshoe vortex consists of two infinitely long vortex fila – pIG 5.4 – p^g eiementary ments of unit strength but opposite signs horseshoe vortex, located infinitesimally close together

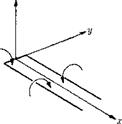along the positive ж-axis and joined together by an infinitesimal piece along the y-axis, also of unit strength (see Fig. 5-4).

The solution for this can be obtained by integrating the solution for a doublet in the ж-direction. Thus /•00

г___ 1 / г dxi _ 1 г Л x

* ~ J* (xj + y + z2)3/2 47r У2 + г2 y/x*

(5-35)

To extend these solutions to compressible flow the simplest procedure is to notice that by introducing the stretched coordinates

У = 0у, г = j8z,

where /3 = /l — M2, the differential equation (5-29) transforms to the Laplace equation expressed in the coordinates x, y, z. Hence any solution to the incompressible flow problem will become a solution to the compres­sible flow if у and z are replaced by у and z. This procedure gives as a solution for the simple source

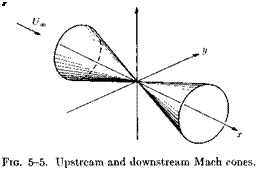
This solution could be analytically continued to supersonic flow (M > 1). However, the solution will then be real only within the two Mach cones (•y/M2 — l)r < x (see Fig. 5-5), and for physical reasons the solution within the upstream Mach cone must be discarded. Hence, since we must discard half the solution it seems reasonable that the coefficient in front of it should be increased by a factor of two in order for the total volume
output to be the same. Thus the solution for a supersonic source would read

J___________ 1_________

2ir Vz2 – (М2 – l)r2

A check on the constant will be provided in Chapter 6.

The use of the elementary solutions to construct more complicated ones is a method that will be frequently employed later in connection with three-dimensional wing theories. This method is particularly useful for developing approximate numerical theories. However, in the two-dimen­sional cases that will be considered next as illustrations of the linearized wing theory a more direct analytical method is utilized.