Unsteady Flow Solutions for a Wing with Endplates

To analyze the transient modes of motion of a wing-in-ground-effect vehicle (takeoff, landing, variation of ground clearance, etc.), as well as to evaluate the influence of wind-wave perturbations, it is useful to have the unsteady characteristics of the main lifting surface. To obtain the corresponding solu­tions for the case of a schematized flying wing configuration in the form of a rectangular wing with endplates in the extreme ground effect, one has to solve equation (4.53) with boundary conditions (4.54) and (4.57) and initial condition (4.58).

4.4.1 A Nonlinear Unsteady Solution for Small Gaps Under Endplates

If one assumes that the relative gap under the endplates is sufficiently small at any moment, i. e.,

(*^5 t) Л h(t)

where h(t) is the instantaneous distance of the trailing edge from a corre­sponding point on the ground and G is the generalized gap parameter intro­duced earlier, it is possible to derive an approximate solution of the nonlinear unsteady problem of the flow past a wing with endplates, by iterating on a leading-order solution for G = 0. If one assumes that

$(x, t,G) = 4>0{x, t) + 4>i{x, t,G) + 0(G2), 4>i(x, t,G) = 0(G),

then the equation for the first-order contribution of the gap under the end­plates to the velocity potential will be

+

where

. , ,ч ГГ, л2 (дФо2 0дфо

м*.і> = т -(ж) -2-дг

The boundary conditions for ф at the edges will be

(4.106)

The appropriate initial condition for equation (4.104) is

дфі

dx

As seen from the preceding equation, to find the unsteady characteristics of the lifting system for the case of a nonzero gap under the endplates, it is necessary to begin with the solution of the unsteady aerodynamics with no leakage from under the endplates (zero gap), i. e., find ф0(х, t). Such a problem in itself represents a certain practical interest for considering the takeoff of a vehicle from water, because the gaps under the endplates are very small from the begining of motion until almost the moment of detachment from the water surface. In the case of zero gap under the endplates, the problem of determining the potential 4>0(x, t) of the relative motion of the fluid takes the form

W-(^) -25?

0(l, t) = 0,

Ґ dh* Ci(t)

h* (x, t)’

Integrating (4.107) twice, we derive the following expressions for the channel flow velocity and potential:

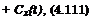– Г dzi fXl dh* Гх

where, as previously, h* = h*(x, t) is a distribution of the instantaneous gap between the lower surface of the wing and the ground. Functions of time Ci(t),C2(t) are to be determined by using the boundary conditions (4.108) and (4.109). Imposing the leading edge condition, we obtain

C2(t) = 0. (4.112)

Satisfying the trailing edge condition (4.109) and taking into account ex­pressions (4.110) and (4.111), we can obtain the following nonlinear ordinary differential equation for determining the function of time C(t):

Ci(t) + a(f)Ci(f) + Ь(*)Сі(*)2 + Ф) = 0 (4.113)

2 5fh*(0,t)

where the “dot” indicates differentiation with respect to time and functions a(£), 6(£), and c(t) are given by

d£ dxi

h*(xi, ty

Differential equation (4.113) is known as a Ricatti equation and cannot be integrated analytically. However, it can be integrated numerically with an appropriate initial condition. To formulate the initial condition with respect to the time function C(t), suppose that at t = 0 the vehicle is at rest and the rate of variation of the ground clearance is equal to zero, i. e., /i*(x,0) = 0. Then, the initial condition for Ci(£), corresponding to zero relative velocity of the fluid in the channel, should be

Ci(0) = 0.

2 dx /i*2(x, t)

Having solved the Ricatti equation (4.113) numerically, we can determine the aerodynamic coefficients. For example, the lift coefficient will be expressed by the following formula:

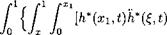
d£ dxi h*(xi, t)2

This solution permits calculating the unsteady nonlinear aerodynamics for the different laws of motion and the deformation of a simple flying wing configuration for a zero gap under the endplates. For example, for a flat wing advancing along the ground and, at the same time, performing unsteady vertical and angular motions, the instantaneous distribution of the relative ground clearance chordwise can be represented by the expression

h* (x, t) = h(t) + 0(t) x,

where h(t) is the time-dependent relative ground clearance at the trailing edge and 6(t) is the current pitch angle.