Unsteady Perturbation of a Steady Flow

To analyze the linear dynamics of a lifting configuration in the ground ef­fect one needs derivatives of the aerodynamic coefficients with respect to the relative ground clearance h, the pitch angle 0, and their rates h and 6. To determine these derivatives, we consider small unsteady perturbations of a
nonlinear steady-state flow. Such a perturbation analysis enables us to re­tain the nonlinear dependence of the aerodynamic derivatives upon basic steady-state parameters, e. g., adjusted pitch angle, relative ground clearance in cruise, etc. As an example of an application of such an approach, take the case of a rectangular wing with endplates at h -» 0. For simplicity, consider full opening of the flap at the trailing edge, that is, 5{ = 1. Represent the velocity potential of the relative motion, the local ground clearance distribu­tion, and the gap under the endplates in the following way:[23]

Ф(х, і) = фа(х) + <j>(x, t), h*(x, t) = hs(x) + h(x, t),

5ep(x, t) = Sep(x) + h(x, t),

where subscript “s” designates steady-state parameters, whereas the second term in each equation represents unsteady contributions.

Substituting the perturbed quantities in (4.53) and accounting for the description of the steady-state flow problem,

we obtain the following equations for the unsteady flow potential ф(х, і):

When deriving the trailing edge condition for unsteady flow potential in (4.118), it was taken into account that d<j>s/dx = — 1 at x = 0. Using the steady flow equation, we obtain an alternative equation for the perturbed unsteady velocity potential:

Having fulfilled the linearization of unsteady flow with respect to non­linear steady flow, we can consider separately two practical cases of height perturbation and pitch perturbation.

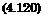Unsteady Height Perturbation. In the case of height perturbation, h(x, t) = h(t). The perturbation potential can be represented as

ф(х, і) = 4>h(x) h(t) + 4>h(x) h(t).

Assume that the gap under the tips of the endplates in cruise is constant chordwise 5ер(я) = 5ep = const. Corresponding equations for the components of the perturbed solution can be derived in the form

Imposing conditions at the leading edges, we arrive at the following boundary conditions at x = 1 for equations (4.121) and (4.122):

Assuming an oscillatory character of perturbations,9 we relate heave accel­eration and heave displacement, namely, h = —k2h, where к = ujC0/U0 is the Strouhal number based on the chord of the wing. Therewith, we obtain the following boundary condition for the derivatives of the unsteady velocity

+ *v) =0, (^-/) =o. / x=0 dx / x=0

potential with respect to h and h at the trailing edge:

Integrating equations (4.121) and (4.122) and accounting for the boundary conditions (4.123) at the leading edge gives the following expressions for the corresponding perturbation velocities and potentials:

. d Фк h dx	_c1-vs(x) vs(x) hs(x) 5e p		(4.126)
	^d фк C2 — x dx hs(x)		(4.127)

Aperiodic perturbations can be analyzed on the basis of the Fourier integral.

To determine the constants c and C2, we apply the boundary conditions (4.124) at the trailing edge. This gives

a + k2 [3 7 (5-а 7

1 + k2 72 ’ 2 1 + k2 72 ’

where

In these expressions, h is the relative ground clearance measured from the trailing edge, Sep = 5ep/h = 0(1), hs(x) = hs(x)/h = 0(1), and vs(x) = d(j)s/dx is the span-averaged channel flow velocity.

The derivatives of the unsteady pressure coefficient with respect to h and h can be derived in the form

It can be seen from equations (4.126)-(4.129) that the derivatives ph(x) and

ph(x) are inversely proportional to the relative ground clearance in cruise,

i. e., are of the order of 0(1 /h).

Unsteady Pitch Perturbation. In the case of pitch motions around the center of gravity h(x, t) = 0(t)(x — xcg), the perturbation potential of un­steady flow can be represented as

ф(х, г)=ф50 + фё0. (4.130)

(*^)

— (x 3?cg)*

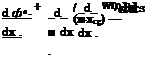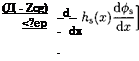The derivatives of the unsteady perturbed velocity potential with respect to perturbation in the pitch в and the rate of pitch 6 are governed by the following equations:

The boundary conditions at the leading and trailing edges for equations (4.131) and (4.132) are

The constants сз and C4 can be calculated by using the boundary conditions at the trailing edge.

The derivatives of the pressure distribution, induced by the unsteady variation of pitch, can be determined by the following expressions:

As in the case of unsteady height perturbations, these derivatives are inversely proportional to the relative ground clearance h in cruise.

Derivatives of lift and moment (around the center of gravity x = xcg) coefficients can be obtained by integrating the derivatives of the correspond­ing pressure distributions:

С0в,§ = (4.138)

Jo

1 – z – ^

(x — xcg) рЬ>М,0(д.) (4.139)

Note that in both unsteady height and pitch perturbations, the derivatives of lift and the moment coefficients with respect to h, /1, 0, and 9 are inversely proportional to the relative ground clearance in cruise.

Now, we turn to determining the drag coefficient Cx and its derivatives with respect to height and pitch perturbations. The drag coefficient can be written as

Cx — CXi + CXf (4.140)

with Cx. and CX{ representing, respectively, induced drag and viscous drag. Later on, it will be assumed that the viscous part of the drag does not vary with small perturbations of ground clearance and pitch angle.

As discussed earlier in this chapter, the induced drag coefficient can be obtained by the formula

CXi=CXp+Cs (4.141)

where CXp is part of the induced drag coefficient due to the longitudinal component of pressure forces, and Cs is a suction force contribution. For flat ground, CXp can be written as

r1 d h[24](x)

CXp(x, t) — h J p(x, t) ^ ■ dx. (4.142)

Substituting h*(x, t) = hs(x) + h(t) + 9(t)(x — xcg) and the perturbation expansion of pressure p(x, t) in (4.143), we obtain the following expressions for the derivatives of CXp in height and pitch:

Ch, h,e, e = h Ґ da._ (4Л43)

p Jo dx

The steady-state pressure contribution to the induced drag is given by

cxp, =h Jo рЛх)А‘dx – (4.144)

We consider the suction force contribution to the induced drag coefficient. According to (4.63), it can be determined as

	Cs = —h h*( 1, t)[l + v(l, t)]2
	= – h[hs + £(U)][1 +us(l) +v(x, t)}2.	(4.145)
where v(x, t)	= дф/дх. Expanding (4.145) to the first order,
	Cs„ = —2hhs(l)[l + vs(l)]2,	(4.146)
	сше = _2hhs(l)[l + Vs(l)]^_ (1).	(4.147)
It can be seen from (4.144) and (4.148) that for h —> 0, the induced drag coefficient is of the order of 0(h). Because hpE — 0(1), it follows from (4.144)

and (4.148) that derivatives of the induced drag coefficient in the extreme ground effect are of the order of 0(1).