Vertical Rate of Descent in a Glide
The vertical rate of descent is the altitude through which the helicopter descends per second (Figure 81). This rate is found from the formula
![]() V і sin 0. gl
V і sin 0. gl
The vertical velocity will be constant for constant glide angle and constant velocity along the trajectory. This means that the propulsive force in a glide is the weight force component = G sin 0. The work of this force per unit time will be power, equivalent to the power required for horizontal flight at a velocity equal to the gliding velocity. Consequently,
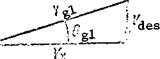
![]() G„V = N, = G sin 0 V. 2 gl h gl
G„V = N, = G sin 0 V. 2 gl h gl
|
|
|
|
|
|
![]()
This means that the work per unit time of the helicopter weight force will be equivalent to the power supplied to the main rotor shaft in horizontal flight at the same velocity with which the helicopter glides in the autorotative regime. From (45) we can find the vertical rate of descent during gliding
|
|
|
|
![]() is the power required for horizontal flight, hp; is the helicopter weight, kgf.
is the power required for horizontal flight, hp; is the helicopter weight, kgf.
We see from (46) that the minimal vertical rate of descent will be achieved
when gliding at the economical speed, since Vgc corresponds to the required
power N. , i. e.
min
75N.
|
||
For rough calculations we can use the approximate formula = l/2Nrat,
![]()
then we must introduce the power utilization coefficient since = N £ Taking the value of this coefficient to be? = 0.8, we find
We note that the ratio G/N = q is called the power loading, and the equality takes the form
![]() ‘a
‘a
des . q.
mm rat
q I’P = E., is the helicopter energy efficiency; ratr M
We substitute this value into (48)
30
des . E
mm M
![]() The average value of the energy efficiency is20 • Then the formula for determining the minimal helicopter gliding vertical rate of descent will be
The average value of the energy efficiency is20 • Then the formula for determining the minimal helicopter gliding vertical rate of descent will be
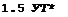 V, = у? =
V, = у? =
des . 20
mm
We recall that this formula is approximate, but it yields adequately precise results, although somewhat low.
Comparison of the vertical rates of descent in glide and vertical descent makes it possible to say that the vertical velocity in the glide will be
2-2.5 times less than in the vertical descent. Therefore, gliding is used in all cases if surrounding obstacles do not interfere.
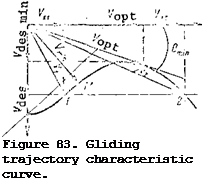
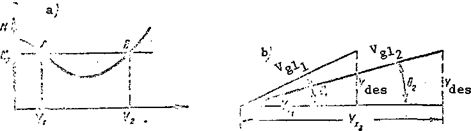
However, gliding can he performed with other velocities along the trajectory rather than the economical velocity. A special graph — the helicopter glide trajectory polar curve — is constructed for determining the gliding velocities and angles. We use the power required and available curves for horizontal flight to construct this graph. If we draw on these curves a straight line parallel to the horizontal axis, it crosses the power required curve at the points A and В (Figure 82a). The point A corresponds to the horizontal flight velocity V^,and the point В corresponds to the velocity 4 .
We take these velocities as the horizontal components of the gliding velocity (Figure 82b): V1 = V ; V„ = V. Since these velocities correspond
to one and the same power required for horizontal flight, we use (46) to find the vertical descent velocity. It will be the same for gliding with the velocities V and V. After determining V, and V, we find the gliding
Xj X£ QcS X
velocity
Then we find the gliding angle
![]() Conclusion: the same vertical rate of descent corresponds to two gliding
Conclusion: the same vertical rate of descent corresponds to two gliding
regimes with large and small gliding angle, with high and low velocity along the trajectory. We usually select gliding with the lower angle but the higher velocity along the trajectory. After making these calculations for several vertical velocities, we plot the helicopter glide polar (Figure 83). From this plot we can find:
— the minimal vertical rate of descent;
— 
 |
the minimal gliding angle which corresponds to the velocity V , numerically equal to the optimal horizontal flight speed;
— the vertical velocity in a vertical descent (point of intersection of the polar curve with the vertical axis).
If we draw through the polar a secant parallel to the horizontal axis, the points of intersection 1 and 2 will correspond to two gliding regimes, for which the vertical rate of descent will be the same and the velocities along the trajectory will be different. The point M on the polar corresponds to the minimal velocity along the trajectory.











