CONSTANT-POTENTIAL (DIR1CHLET BOUNDARY CONDITION) METHODS

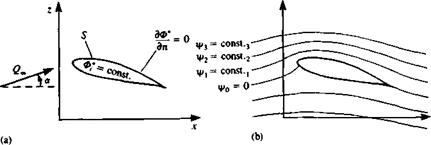
In the previous examples the direct, zero normal velocity (Neumann) boundary condition was used. In this section similar methods will be formulated based on the constant-potential method (Dirichlet boundary condition). This condition was described in detail in Section 9.2 and in principle it states that if дФ*/дп = 0 on the surface of a closed body then the internal potential Ф,* must stay constant (Fig. 11.25a)

Ф,* = const. (11.56)

It is possible to specify this boundary condition in terms of the stream function 4х (Fig. 11.256) and in this case the body shape is enclosed by the stagnation streamline where 4х = const, (which may be selected as zero). Many successful numerical methods are based on the stream function and they are very similar to the methods described in this chapter. Also, the stream function can describe flows that are rotational, but an equivalent three-dimensional formulation of such methods is nonexistent. Because of the lack of three – dimensional capability, only the velocity potential-based solutions will be discussed here.

Following Chapter 9, the velocity potential can be divided into a free-stream potential Ф* and perturbation potential Ф, and the zero normal velocity boundary condition on a solid surface (internal Dirichlet condition) is

Ф* = Ф + Ф* = const.

Placing the singularity distribution on the boundary S (and following the two-dimensional equivalent of Eq. (9.10)—see Eq. (3.17)) this internal boundary condition becomes

Ф*(х, z) = -^- f In (In/■)]*/£ + Ф„ = const. (11.57)

FIGURE 11.25 Methods of fulfilling the zero normal velocity boundary condition on a solid surface.

and when the point (x, z) is on the surface then the coefficient 1/2л becomes 1 /л.

This formulation is not unique and the combination of source and doublet distributions must be fixed. For example, source-only or doublet-only solutions can be used with this internal boundary condition, but when using both types of singularity the strength of one must be prescribed. Also, any vortex distribution can be replaced by an equivalent doublet distribution, and therefore solutions based on vortices can be used too.

To construct a numerical solution the surface S is divided into N panels and the integration is performed for each panel such that

2 — I о In r dS — Ц —- (In r) dS + Ф„, = const.

i=l 2Л./panel j=1 2л /panel on

The integration is limited now to each individual panel element, and for constant, linear, and quadratic strength elements this was done in Chapter 10. For example, in the case of constant-strength singularity elements on each panel the influence of panel / at a point P is

(11.58)

in the case of a doublet distribution and for a source distribution

(11.59)

Once these influence integrals have been evaluated (as in Chapter 10) the boundary condition inside the surface (at any point) becomes

N N

X BjOj + X Cjfij + Фоо = const. for each collocation point (11.60)

y = l /=1

By a specification of this boundary condition on N collocation points, N linear equations can be created.