Effect of Mean Flow

To test the efficacy of the inviscid solid wall boundary condition in the presence of a mean flow, this acoustic pulse problem is modified to include a uniform stream of Mach number 0.5 flowing parallel to the wall. In this case, the reflection process is modified by the effect of mean flow convection. For this problem, a computational domain -100 < x < 100, 0 < y < 200 is used. The wall is at y = 0. The linearized Euler equation in two dimensions is as follows:

	p		Mp + u		v
d	u	d + dx	Mu + p	d + 9 y	0
dt	v	Mv	P
	p		Mp + u		v

= 0,

where M = 0.5. The initial conditions are

t = 0, u = v = 0

The exact solution of this problem is available. Let

a = (ln2)/25, n = [(x – Mt)2 + (y – 25)2]2, g = [(x – Mt)2 + (y + 25)2]1.

Figure 6.14. Pressure waveforms of an acoustic pulse reflected off a solid wall along the line x = y.

The solution is

TO TO

и = 0.01 ^ 2qM^ / e 4a sin^^г )J1 df + 0-01 ^ e- 4“ sin(^tJ (f^)f df

0 0

TO TO

(y — 25) f2 (y — 25) f2

v = 0-01 yon – e— 4a sin(ft)J1 (fn)f df + 0.01 y^ e— 4a sin(ft J(fg)f df

00

TO

0-01 f2

p = P = ~2a e 4a cos(ft)[J0(fn) + J0(fs0]fdf,

0

where J0(z), J1 (z) are Bessel functions of order 0 and 1.

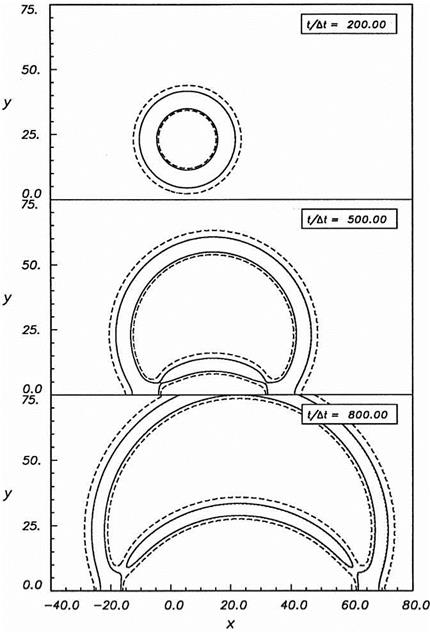
Figure 6.15. Pressure contour patterns associated with the reflection of an acoustic pulse by a solid wall in the presence of a Mach 0.5 uniform mean flow.

Figure 6.15 shows the computed pressure contour patterns of the acoustic pulse, with the use of the 7-point DRP scheme, at 200, 500, and 800 time steps. Again, the computed pressure contours are indistinguishable from those of the exact solution. Geometrically, the pressure contour patterns are identical to those without mean flow (see Figure 6.13). The uniform mean flow translates the entire pulse downstream at a Mach number of 0.5. The good agreement between the computed and the exact

solutions suggests that the ghost point numerical boundary conditions can be relied upon to simulate correctly a solid boundary even in the presence of a flow.