Interior noise radiation and vibration of the shell structure

To effectively establish the interior sound radiation and global flexural response of the enclosing flexible wall, it is convenient to express the two phenomena in terms of energy functions, which embrace in a single term the spatially distributed characteristics of the sound and flexural vibration fields. Moreover, the stochastic nature of the disturbance pressure field exerted by the TBL fluid flow necessarily leads to the expression of these energy functions in terms of concepts and formulations for random processes. Thus a particular formulation is presented below, which refers to a similar study proposed by (Gardonio et al. 2012) and considers the formulation for stationary stochastic processes given in (Bendat and Piersol 2000).

The overall sound radiation to the interior of a cavity can be established in terms of the time-averaged total acoustic potential energy Ep, which can be expressed as follows (Nelson and Elliott 1992):

where the instantaneous total acoustic potential energy is given by Ep(t) =tjt I p(xc, t)2dV. For stationary and ergodic processes, such as the

•R 2pG0 *V

interior sound radiation induced by the pressure field due to a fully developed TBL, this quantity can be derived in terms of a “Power Spectral Density” (PSD) function of the total acoustic potential energy [27]Ep(<$

— 1

Ep = —J SEp (®)d® . (44)

In

Normally, in acoustics, rather than considering the averaged function, the corresponding frequency spectrum is studied, which can be plotted graphically and provides a deeper insight on the physics of the sound radiation phenomenon under study. According to (Bendat and Piersol 2000), the PSD of the total potential energy SEp(m) can be derived starting from the following expression:

-®2 + j2^a,„®a,„®)

where the superscript * indicates the complex conjugate, E[…] denotes the expectation operator. The interior pressure can be derived from Eq. (19) with vn (xs) = w(xs), where Gc (xc | xs) is given by Eq. (22) and w(xs) is derived from Eq. (26), so that

Thus, after some mathematical manipulations, the PSD of the total acoustic potential energy can be expressed with the following matrix relation

Here Y = [- o2M + ja>Z + k]-1 is the structural modal admittance matrix that can be derived from Eq. (42). Also, Q is the acoustic modal impedance matrix whose elements are given by

Finally, the elements of the Spp(«) matrix with the modal excitations PSDs are given by

where STBL(xs, xS,«) is the spatial cross spectral density of the TBL blocked pressure field between points xs -(x, y) and x’s -(x, y):

STBL (xs, xS,®) = limE[1 P*(xs,®)P(xS,®)] . (51)

T T

Chapter 6 of this book presents an overview of the models and formulations for the spectral density of the pressure field produced by a TBL fluid flow on a rigid wall. Additional review material can be found in references (Blake 1986; Leehey 1988; Bull 1995; Graham 1997; Howe 1998; Cousin 1999; Maury et al. 2002b; Hwang et al. 2009).

The analysis of the sound radiation to the interior is often contrasted with the flexural response of the shell enclosure, which can also be represented in terms of a single function. In fact, the overall flexural vibration of the shell can be

established in terms of the time-averaged total flexural kinetic energy Ek, which can be expressed as follows:

Ek = hm — j 7 jS Pshw(x,,t) dSb dt, (52)

T – T/ 2 b

where the instantaneous total flexural kinetic energy is given by Ek (t) = -1 f pshxv(xs, t)2 dSb. As seen with the interior sound radiation, for

JSb

stationary and ergodic processes this quantity can be derived in terms of the PSD functions of the total kinetic energy SEk(a):

— 1 г+»

Ek = 2^1-»SEk (m)dm ’ (53)

where

Also, in this case, the orthonormality property of the structural natural modes leads to the following simple matrix expression

Seu = 2 M®[28]Tr [Sbb (®)], (55)

where the matrix Sbb (®) with the self and mutual PSDs of the structural modal responses is given by:

As discussed at the beginning of this section, the space-frequency domains formulation presented above can also be developed in the wavenumber- frequency domain. For instance, as discussed in Chapter 6, the spatial cross spectral density of the excitation field can be expressed in terms of the wavenumber spectral density function STBL (k,®) by means of inverse space – Fourier transform such that:

і +Х4-»

STBL Os > XS >0 і і STBL (КФМХ-ХУ2k, (57)

(20

where the vector k contains the wavenumber components in the stream-wise and cross-wise directions of the fluid flow. Substitution of this expression into Eq. (50) leads to the following expression for the elements of the matrix with the modal excitations PSDs

Spp,™(ffl) = JS jS, C(xs) 77Stbl(k, ffl)Ck(x-x,)d2k £(*’,)dSbdS’b

2Я)

1 +да +да

І R“(k)Stbl(k, ffl)^(k)*d2k

(2 я-)

where the shapefunctions </>“(to, m) are given by the space-Fourier transforms of the natural modes:

CO) = lt C(xsVMdSb. (59)

Here the integration is restricted to the surface of the structure Sb since C(xs) = 0 for xs g Sb. Eq. (58) highlights how the wavenumber approach leads
to a formulation where the frequency-dependent modal excitation produced by the TBL fluid flow, Spp(m), is given by the unbounded integral in the

wavenumber domain of the product of the wavenumber spectral density function for the excitation field STBL (k, a) and the wavenumber spectrum of the natural

modes C(k,®), ie. the shape functions. Thus it can be interpreted as the result of a filtering effect between the wavenumber spectrum of the excitation field and the wavenumber spectrum of the natural modes.

The spatial Fourier transform approach can be extended also to the early part of the formulation presented above for the derivation of the total potential energy PSD, SEp(m), and total kinetic energy PSD SEk(®). In this case, as shown by

Mazzoni (2003) and Maury et al. (2002a), the PSD functions are derived from the wavenumber integrals of the products of wavenumber spectra for the TBL excitation, the modal shapes and the structural-acoustic modal response functions. With this “full wavenumber” approach, the structural response and interior sound radiation are thus derived as the product of wavenumber spectra for the excitation, modal couplings and structural and acoustic responses, each producing a specific filtering effect. This appears to be a very interesting and appealing approach for studying the response of a system, although some practice is required to produce accurate analyses. 2

Figure 7. Model problem composed of a baffled flexible panel, which is excited
by a TBL pressure field on the outer side and radiates sound on the inner side.

— 1 +7 2

Pr = I is ^ ’t)P(Xs ’t)dSb dt

T I sb

-Tf 2 b

Here the spatial integral is for the instantaneous total radiated sound power
Pr(t) = f w(xs, t)p(xs, t)dSb (Fahy and Gardonio 2007). As discussed in the previous

Sb

section, assuming the process is stationary and ergodic, this quantity can be derived with the following relation:

1 г+»

Pr = f Spr(®)d® , (61)

In’1

where the PSD function of the total radiated sound power SPr(a) is given by (Gardonio et al. 2012):

The complex velocity w(xs, a) can be derived from the modal expansion of the transverse displacement, which is given by Eq. (25c). Also, as discussed in

Section 1.2, the sound pressure over the surface of the panel can be derived from the Rayleigh integral given in Eq. (12) assuming[29] vn (xs) = – W(x s), so that

Substituting this equation into Eq. (62) and considering the modal expansion for the panel velocity derived from Eq. (25c), after some mathematical manipulations, the following expression is derived for the radiated sound power PSD

S Pr = 2 ®2Tr [A(®)Sbb (»)]

where a(®) is the power transfer matrix that defines the sound power radiated by single modes (diagonal terms) and pairs of modes (off diagonal terms). For a flat rectangular panel the power transfer matrix is given by (Fahy and Gardonio 2007)

A(да) = t4s (xs)кгт-фr(xs )dSbdS’b

4 л Jsb Jsb kd

where d =|xs – Xs | is the distance between point xs and point x’s. Also, the matrix Sbb(0) with the self and mutual PSDs of the modal responses is given by

where the structural modal admittance matrix Y is obtained from the modal equations of motion of the plate structure. More specifically, as seen for the cylinder structure, the unknown complex modal amplitudes br, m are derived by

substituting Eq. (25c) into Eq. (24c) with the differential operator L3 (…) for flexural vibration of thin flat plates (Graff 1975; Cremer et al. 1988; Reddy 2006). The resulting equation is then multiplied by a m – th mode and integrated over the surface of the plate so that, using the orthonormality property of the natural modes and assuming hysteretic structural damping, the following set of uncoupled ordinary equations is obtained:

Mp (<m (1 + jtf) – Km = fr, m, (67)

where M p is the mass of the panel and fr, m is the да-th modal excitation term, which is given by

fr. m =Sbfr O’sM-m 0’s)dSs • (68)

For a flat rectangular thin panel, the natural frequencies and natural modes are given by:

where mp =Pphp, Mp =PphplXplyp and Bp = ЕркЦ[l2(l-vj;)], assuming Pp, Ep

and vp are respectively the density, Young’s modulus of elasticity and Poisson’s

ratio for the material of the plate. Finally, m1, m2 are the indices in the x and y directions for the m-th mode. As seen in Section 1.5, the set of Eqs. (67), can be casted in the following matrix expression

[-®2M+K(1 + ]фьг = f, (70)

where the diagonal elements of the mass and stiffness matrices are given by Mmm = Mp and Kmm = Mpa]m respectively and the elements in the modal response and excitation vectors are given by brm = brm and frm = frm respectively. Thus, the structural modal admittance matrix is given by Y = [-®2M + K(1 + jq)Y. In summary, for the simplified model problem considered in this section, the flexural response and interior sound radiation are studied using Eqs. (55) and (64) respectively. The modal amplitudes are derived by substituting Eq. (25c) into Eq. (24c), which, for a flat plate structure, is uncoupled from Eqs. (24a, b) for the in-plane vibration (Soedel 1993). According to Eq. (55) the spatially averaged response of the structure depends on the squared modal responses, which, in turn, depend on the coupling between the distributed excitation field and the natural modes. As illustrated in more detail in the following subsection, the TBL pressure field efficiently couples with all modes. In contrast, for example, a plane acoustic wave incident at a given angle with the normal axis to the plate, tends to couple efficiently with the so called volumetric modes which are characterised by a non-zero spatially averaged displacement and thus have both mode orders odd. Eq. (64) shows that the radiated sound power PSD depends on the squared modal amplitudes weighted by the diagonal terms of the matrix a (®) and on the products of pairs of modal amplitudes weighted by the appropriate off-diagonal terms of the matrix a(®).

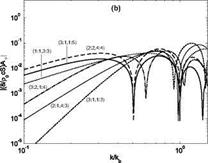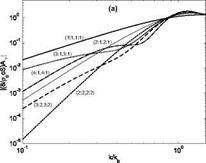
Figure 8. Self (a) and mutual (b) radiation efficiencies of the rectangular panel

natural modes.

In other words, sound radiation occurs both via self radiation effects of each mode and the cross radiation effects of pairs of modes. Figure 8 shows both the diagonal (plot a) and off-diagonal (plot b) elements of the matrix a (®) for the panel considered in the next subsection with reference to the ratio between the acoustic and flexural wave numbers k/kb. Plot (a) indicates that, at low frequencies such that k<kb (i. e. for subsonic flexural waves such that cb <c, where cb =4a>(Bp/mp )^4), the self radiation effect of each mode is rather weak and

tends to increase with frequency until it reaches the maximum value around k/kb =1 (i. e. for sonic flexural waves with cb = c). Volumetric modes

characterised by both odd mode orders tend to radiate sound more efficiently than other modes. Also, the radiation efficiency tends to decrease as the mode orders raise. For frequencies such that k >kb (i. e. for supersonic flexural waves with cb > c) all modes become efficient radiators of sound. Plot (b) shows that the mutual radiation effects are comparatively smaller than the self radiation effects, particularly at higher frequencies such that k > 0.5kb. Also, the curves in

the graph are characterised by sharp dips around certain values of the ratio k/kb, which are due to the fact that the off diagonal terms in matrix a (®) alternate between positive and negative values and thus their moduli go to zero at certain values of the ratio k/kb (Fahy and Gardonio 2007). This interesting finding

indicates that for certain frequency bands, the mutual sound radiation effect of pairs of modes may be either positive or negative; in other words it may enhance or reduce the total sound radiation. Therefore, reducing the response due to some
specific modes could lead to reductions of sound radiation at given frequency bands, but to the enhancement of sound radiation at other frequency bands (Fuller et al. 1996).