Physics of TBL sound radiation by a baffled panel
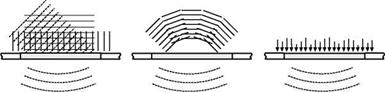
In order to better understand the physics of the interior sound radiation generated by a TBL pressure field on the panel (Figure 9d), three typical sound radiation problems are considered first, which are due to the following excitation fields acting upon the panel: a) the fully correlated pressure field generated by a time – harmonic “acoustic plane wave” (APW) with grazing, 45o and normal angles of incidence (Figure 9a); b) the partially correlated pressure field generated by an “acoustic diffuse field” (ADF), which is composed by a random distribution of plane waves whose energies are equally divided over all angles of incidence (Figure 9b) and c) the fully uncorrelated pressure field due to the so called “rain on the roof’ (ROR) random excitation, which is characterised by a uniform distribution of point forces totally uncorrelated between each other (Figure 9c). The panel is assumed simply supported along the perimeter and its dimensions and material properties are summarised in Table 2.1. An extended version of this analysis can be found in (Rohlfing and Gardonio 2009).
The panel response and the sound radiation produced by the ADF, ROR and TBL excitations are analysed in terms of the total kinetic energy PSD and total radiated sound power PSD, derived with the formulation presented in the
|
(a) acoustic plane waves (b) acoustic diffuse field (c) rain on the roof
|
|
(d) TBL excitation
|
Figure 9. Sound radiation induced by: a) APW at grazing, normal and 45′
incidence angles, b) ADF, c) ROR and d) TBL.
|
Parameter |
Value |
|
dimensions |
lxp y-lyp = 278k247 mm |
|
thickness |
hp =1.6 mm |
|
mass density |
Pp = 2720 Kg/m3 |
|
Young’s modulus |
Ep = 7×10і0 N/m2 |
|
Poisson ratio |
Vp = 0.33 |
|
Structural loss factor |
r/~ 0.02 |
|
Table 2.1. Geometry and physical parameters for the panel. |
previous section. For the fully correlated time-harmonic plane wave acoustic excitations, the panel response and sound radiation are instead investigated with reference to the spectra of the time-averaged total kinetic energy Ek (®) and
 |
time-averaged total radiated sound power Pr (®). These two frequency-
Pr(®) = — f Refit(xs,®)*p(xs,®)ldSb =®2b (a)HA(®)b (a) , (72)
2 JSb
where the vector br(o) is derived from Eq. (70). The pressure field over the surface of the panel produced by an acoustic wave with azimuthal and elevation (with reference to the normal of the plate) angles, ф and в respectively, can be expressed as:
PApw&, t) = RejpAPwH ei(0t-W) } , (73)
where pAPW(й) is the complex amplitude of the incident wave and kx = k sin(<9)cos(0), ky = k sin(#)sin(^) are the wave number components in x and y
directions. Thus, the incident acoustic plane wave produces a waved pressure field on the panel whose wavelength is given by ^sin0. For instance, as schematically depicted in Figure 5a, for grazing angle of incidence such that
в=9C°, the waved pressure field acting on the panel is characterised by the same wavelength as that of the incident acoustic field. When the angle of incidence turns to в = 45°, the wavelength of the pressure field acting on the panel becomes V2 times longer than that of the incident acoustic wave. Finally, if the angle of incidence is further reduced towards 6=0° the projection of the acoustic wavelength into the plane of the plate tends to infinity and thus the pressure field is no more waved and becomes spatially uniform. Moving back to the formulation for the response and sound radiation of the plate, considering the excitation pressure field given in Eq. (73), the modal excitation terms frm in Eq.
(68) result (Wang et al. 1991):
![]() (®) = (x У) Cj( = 4 pAPW(m) lxpln
(®) = (x У) Cj( = 4 pAPW(m) lxpln
where, if ”л^ + sinffcosifi(aixplc°) and ”л^+sindsi^^^jc,),
and, if ”л = + sin^cos^M^/c,) and т2л = + sin0sin^(ftlyp/c°),
The response and sound radiation produced by the other three types of excitations are instead analysed in terms of the total kinetic energy PSD and total radiated sound power PSD derived with the formulations presented in Sections
1.6 and 2 respectively. Thus the excitations are expressed in terms of cross spectral density functions. The cross spectral density for the diffuse sound field excitation is assumed
c / > , s / sin kd
SADF (x s, Xs,®) = SADF (») ^ (77)
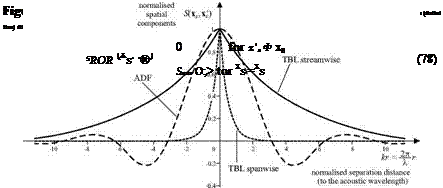
where in this case d =|xs – Xs | is the distance between the two points x s and x’s and SADF(m) is the PSD of the ADF excitation at any point on the panel. Thus the ADF cross spectral density function is the same in all directions and is characterised by the so called “sinc” function which is shown by the dashed line in Figure 1C. For the fully uncorrelated rain on the roof excitation, the cross spectral density is assumed as
where, in this case, SROR(a) is the PSD of the ROR excitation at any point on the panel. Thus the cross spectral density is characterised by a delta function. As discussed in Chapter 6, the cross spectral density for TBL excitation is derived from the Corcos model, so that (Corcos 1963a; Corcos 1963b; Corcos 1967)
![]()
 |
STBL (xs, x’s M = Stbl OK1
where Stbl(o>) is the PSD of the TBL excitation at any point on the panel, rx and ry are the x and y components of the distance between points xs and x! s, Lx = aJJjсо and Ly =ayUcjсо are the correlation lengths in x and y directions and Uc is the convective velocity, which is normally derived from the relation Uc – KUm, with 0.6 <K<0.85 (Cousin 1999). In this study, the convective velocity is assumed to be Uc – 0.6U„, where the free flow velocity is taken as U„= 225m^s. Also, as indicated in references (Maury et al. 2004; Elliott et al. 2005), the empirical parameters ax and ay are assumed to be 1.2 and 8
respectively. According to Eq. (79), the TBL cross spectral density function varies with direction and is characterised by two exponentially decaying functions in the stream-wise and span-wise flow directions. In the stream-wise direction, the convective effect also produces a waved profile of the cross spectral density function. The solid and dotted lines in Figure 10 show that the span-wise component decays more rapidly than that in the stream-wise direction. This is due to the fact that the correlated pressure field produced by each vortex in the turbulent fluid flow is smeared in the direction of the flow by the motion of the fluid.
The comparative analysis of the structural response and sound radiation produced by these four types of excitations will be carried out considering the spectra of the time-averaged total kinetic energy and of the time-averaged total radiated sound power produced by the APW excitations with unit amplitude, i. e. PAPW(a) = 1. Also the spectra of the total kinetic energy PSD and total radiated sound power PSD produced by the ADF, ROR and TBL excitations will be considered assuming they have unit PSD, i. e. SADf(a) = SRR(a) = STB1(a) = 1. In this way the specific characteristics of the structural response and sound radiation produced by the TBL pressure field are contrasted with those of the other three excitations independently from the specific energy distribution in frequency of each type of excitation.