Special Techniques
A.1 Methods of Complex Variables
Solutions of two-dimensional, incompressible, potential flow problems can be obtained using functions of complex variables. In the following we follow Moran [1] and others [2].
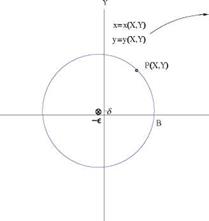
A complex number z consists of two real numbers x and y, where
z = x + iy, Z = x – iy, i = 1 (A.1)

or
 |
|
On the other hand, if Az = i Ay, then
The two conditions of Eq. (A.9) are known as the Cauchy-Riemann equations. In general, since x = (z + z)/2 and у = (z — z)/2i, w(x, y) = w(z, z). In fact
![]() дw 1 дф дф i дф дф
дw 1 дф дф i дф дф
дz 2 дх д у + 2 д у + дх
Therefore, for analytic functions, дw/дz = 0, i. e. w is a function of z only.
If w(z) possesses a derivative at z = z0 and at every point in some neighborhood of z0, then w(z) is said to be analytic.
Let
![]() дф дф дф дф
дф дф дф дф
дх д у ’ д у дх
then
= u — i v (A.12)
dz
is the complex velocity.
It will be shown later that the derivative of an analytic function is also analytic function and hence an analytic function possesses derivatives of all orders and can be represented by convergent Taylor series at any point in the region where the function is analytic (the radius of convergence is determined by the closest point where the function fails to be analytic, i. e. the closest singular point). It follows then for any analytic function w
However,
d2 w 1 д2ф д2ф i d2 ф д2ф
dzdz 4 dx2 + dy2 + 4 dx2 + dy2 ^ ( • )
hence, ф and ф satisfy Laplace equation.
Since, dw/dz is also analytic function, then Eq. (A.12) implies
du dv du dv
dx dy ’ dy dx (A.15)
The first of Eq. (A.15) is the continuity equation and the second is the irrota – tionality condition. Hence ф and ф are the potential and stream functions of twodimensional incompressible, irrotational flows and w(z) = ф(x’ y) + iф(x’ y) is called complex potential. Both the real and the imaginary parts of the above analytic function have continuous second partial derivatives satisfying Laplace’s equation
![]() д2ф д2 ф д2ф д2ф
д2ф д2 ф д2ф д2ф
dx2 + dy2 0 dx2 + dy2
Moreover, the curves of the family ф(x’ y) = constant are the orthogonal trajectories of the curves of the family ф (x’ y) = constant, (and vice versa if ф and ф satisfy Laplace equation, then w(z) is an analytic function).
Examples of complex potential are
(i)
w = Ue iaz = U(x cos a + y sin a) + iU(y cos a – x sin a) (A.17)
The above expression represents the potential and stream functions of a uniform flow making an angle a with the x-axis.
(ii)
1
w = (Q + i Г) ln z (A.18)
2n
This w represents the complex potential of a source of strength Q and a potential vortex of strength Г at the origin.
(iii)
 |
In analytic mapping, the length of infinitesimal segments are altered by a factor I ddW I which depends only on the point from which the segments are drawn (regardless
of the direction). The infinitesimal areas are then magnified by the factor | ddW |2, i. e. by J.
Also, two infinitesimal segments forming an angle will both be rotated in the same direction by the same amount. A transformation which preserves the sense and the magnitudes of angles is said to be conformal. Hence, any analytic function W = W(Z) defines conformal transformation (as long as dW = 0).
An important theorem of conformal mappings is the following: Laplace equation is transformed to a Laplace equation, for example, consider the one-to-one transformation z = z(Z), its inverse Z = Z(z) and the complex potential W(Z) =
Ф(Х, Y) + iФ(X, Y) = w(z) = ф(х, у) + iф(х, y) hence,
in the Z-plane, are transformed to
![]() д2ф d2 ф д2ф д2ф
д2ф d2 ф д2ф д2ф
дх2 + ду2 дх2 + ду2
in the z-plane (where ddZ = 0). Moreover,
ф(х, у) = ф(Х, Y), ф(х, у) = V(X, Y), w(z) = W(Z) (A.27)
The proof is based on the fact that an analytic function of an analytic function is analytic, see [3].
It can be also shown that the kinetic energy of the motion remains constant under conformal transformation, see [2].
Let the derivatives of the complex potentials with respect to z and Z be dw/dz and dW/dZ.
|
![]() dW dw dz dw dW dZ dZ dz dZ ’ dz dZ dz
dW dw dz dw dW dZ dZ dz dZ ’ dz dZ dz
The complex velocity in the Z-plane is defined as
The equality of the moduli yields
hence the velocity magnitude can be found in the physical plane. Since the ratio of two incremental areas in Z – and z-planes is equal to the Jacobian, hence the integral over corresponding domains of the kinetic energy for constant density flows is preserved. Using Bernoulli’s law, this relation can be used to find the pressure distribution anywhere in the physical plane.
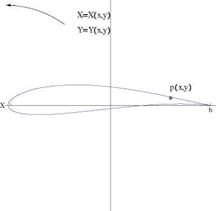
The simplest example of conformal transformation is mapping the circle to a slit, given by
The cylinder of radius r0, centered at (—e, 6) in the Z-plane, passing by the point B (a, 0), maps onto a Joukowski profile, with cusped trailing edge at point b, Fig. A.2. Special cases correspond to є = 0 and/or 6 = 0. In the Z-plane, the flow at angle a with the X-axis, about the circular cylinder, is given by the complex potential
![]()
|
|
||
|
|||
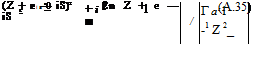 |
||
The complex velocity in the physical plane is given by
There is a singularity at Z = ±a. The singularity at Z = a on the cylinder, is needed to have a cusped airfoil, while the singularity at Z = —a inside the cylinder, is excluded from the domain of interest.
The Kutta-Joukowski condition requires that velocity to be finite at the trailing edge, hence the numerator should vanish at Z = a, meaning that the point is a stagnation point for the flow past the circular cylinder. The condition reads
Г = 4nU ((a + e) sin a + S cos a) (A.36)
![]()
![]()
Note that the condition obtained is the same for the real and imaginary parts of the complex equation dW(a)/dZ = 0 because the flow is constrained to be tangent to the cylinder. After some algebra one finds
There are two important special cases:
(i) e = S = 0, for a flat plate at angle of attack. In this case, r0 = a, z = aeie and
(ii) є = 0, 6 = 0 (say 6 > 0), for a circular arc at angle of attack. In this case, r0 = Va2 + 62, and
Г = 4nU (a sin a + 6 cos a) (A.39)
Cauchy Integral Theorem
The Cauchy integral theorem states that the line integral of analytic function in a simply connected region S around a closed curve C in this region, is zero, i. e.
У w(z)dz = 0 (A.40)
To prove the theorem, let w(z) = ф + iф and z = x + iy, hence
w(z)dz = (ф + i ф)(dx + idy) (A.41)
The integral can be expanded as
w(z)dz = (фdx – фdy) + i (фdx + фdy) (A.42)
C C C
Using Green’s theorem with domain D inside curve C
<j> (фdx – фdy) = – j J dxdy = 0 (A.43)
У (фdx + фdy) = — У У dxdy = 0 (A.44)
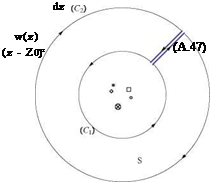
An extension of Cauchy theorem for multiply connected domain where C1 and C2 are closed curves in the region that can be continuously deformed into each other without leaving the region, is given by
w(z)dz – w(z)dz = 0 (A.45)
C1 C2
SeeFig.A.3.
Based on Cauchy theorems, one can show that
1 w(z)
w(z0) = dz (A.46)
2ni z – z0
where z0 is any point in the interior of the simply connected region R whose boundary is sectionally smooth. Moreover, the derivative of w(z) at point z0 is given by
 |
|
Higher derivatives can be obtained formally by repeated differentiation with respect to z0. Finally, the converse of Cauchy theorem is true, namely if w(z) is a continuous function in a region R and if / w(z)dz = 0 for every simple closed curve C which can be drawn in R, then w(z) is analytic in R, see Ref. [4].
Blasius Theorems
The pressure force acting on an element of surface is pds. Assuming unit width, the components in x and y directions are
dFx = – pdy, dFy = pdx (A.48)
Hence, if one defines dF = dFx – idFy, then
dF = – ip(dx – idy) (A.49)
According to Bernoulli formula, p = p«, + pU2/2 – pV2/2 and V2 = (u – iv)(u + iv). On a closed contour, the constant pressure term pOT + pU2/2 does not contribute to the force. Therefore, the elementary force due to pressure reduces to
p
dF = i (u – iv)(u + iv)(dx – idy) (A.50)
But, the complex velocity is related to the complex potential w(z) by
dw
= u – i v (A.51)
dz
Hence
|
The body contour is a streamline along which dw is real since dгф quently, dw is equal to its complex conjugate and can be written as |
= 0. Conse- |
|
d w = (u + i v)(dx — idy) |
(A.53) |
|
Hence |
|
|
p dw p (dw)2 dF = dFx — idFy = i d w = i dz x y 2 dz 2 dz |
(A.54) |
|
The elementary moment about the origin can also be found from |
|
|
dM, o = —— {izdF} |
(A.55) |
|
with the moment counted positive clockwise. Upon integration around the obstacle one obtains |
|
|
F = i P /(dw )2 dz |
(A.56) |
|
M, o=2— {/z (dz) 4 |
(A.57) |
These integrals of analytic functions along closed contour can be evaluated with the theorem of residues.
Far from the obstacle, the velocity perturbation dies out as the flow returns to uniform flow condition. The complex potential can be expanded in a series of inverse powers of z, as
Using as integration contour a large circle of radius R, centered at the origin, one obtains
Integrating term by term one obtains

The integral of moment expands as
Hence, Fx — 0, Fy — (UГ, and M, o — 0. See Ref. [5] for more details. Problem
The objective is to find the potential and stream functions for flow around a corner. Consider the transformation
w(z) — Azn (A.66)
where A is real and n — n/a, 0 < a < 2n.
Using polar coordinate
Therefore
ф = Ar’n/a cos —в, ф = Arn/a sin — в (A.68)
a a
The complex velocity is given by
— = u – i v = – Az{n/a-1) (A.69)
dz a
The streamline ф = 0 is given by в = 0 and в = a. The flow between two planes at angle a are shown in Fig. A.4.
Another example is the flow near the sharp leading edge of a flat plate. In this case the complex potential is w(z) = A*fz, see Fig.A.5.
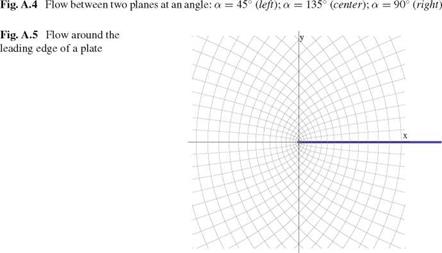 |
Notice that at the origin dw/dz is zero for a < n and dw/dz is infinite for a > n. The origin is a singular point in both cases, see Ref. [5].
TO
E0 — En cos t
n=1
h(Z) = 3 Y + 1 u 1 = const, V Z, Z in SW (4.142)
One can now solve for W(Z, Z) as
W(Z, Z) = 3^+1 (uf – U2^ (4.143)
This result also indicates that the data (Cauchy data) on the C – characteristic (Z, Zi) cannot be specified arbitrarily. Substitution in CR+ yields
3-77+1 (u2 – 2U3) = /(Z), V Z, Z in SW (4.144)
which forces one to conclude that U = U(Z) only, hence W = W(Z) as well. As a result, the perturbation velocity и is constant along the C + characteristics, which are straight lines with constant slope /Y+1)u ■
The subdomain SW is called a simple wave region and we can state that in plane supersonic flow, a region adjacent to a uniform flow region is a simple wave region. This result has been extended to the Euler equations in 2-D, see Courant and Friedrichs [8].
[3] 3
^/t+T u (Z)3
[5] CL2D——- bc—— = 2~f
d
[6] 2cd + 2cd 1 Cl,2D
[7] = 2,…, j = 2,…, jx — 1 (8.40)
Backward differences are used for the first derivative of u in x
L = 2pV2S Cl = W
[9]2