AXIAL FLIGHT: BLADE ELEMENT THEORY

Simple momentum theory treats the rotor as an actuator disk through which a uniform flow passes. Unfortunately this theory tells us little about the flow around the individual blades that make up the rotor system. Momentum theory cannot, therefore, be used to predict the magnitude of any losses associated with realistic flow around rotor blades. Blade element theory overcomes some of the restrictions inherent in momentum theory as it is based upon the idea that the rotor blades function as high aspect ratio wings constrained to rotate around a central mast as the rotor system advances through the air. As before our study of blade element theory begins with purely axial flight.

2.2.1 Elemental forces, thrust, torque and power

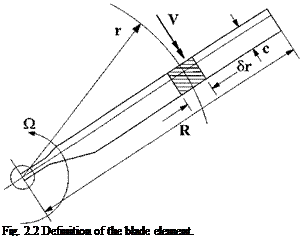
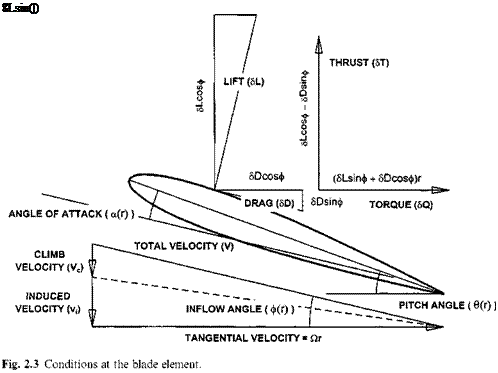
Consider a rotor consisting of b blades climbing at speed Vc. The blades are each of length R, and turn at a rotational speed of ) rad/s. If we now examine the forces generated on a small element, Sr, of a blade located at r from the hub we can gain insight into how a complete rotor system generates thrust and drag. Figure 2.2 shows a blade element and Fig. 2.3 depicts the forces acting on such an element. Each element of the blade is assumed to develop the full aerodynamic forces and moments as it would in two-dimensional flow at the same conditions that occur at its radial station. No allowance is made at this stage for finite span or blade wake effects.

Firstly, we must determine the total flow through the disk. As we have seen for a rotor in a climb this is composed of the climb velocity, Vc, and the induced velocity v;. The resultant velocity at a blade element therefore has a vertical component, Vc + v;, and a horizontal component )r. From Fig. 2.3 it can be seen that the resultant velocity, V is given by:

V = V(Vc + v; )2 + )2r2

This is commonly approximated to V = )r. Justification for this approximation can be seen by considering the example helicopter in a rapid vertical climb (2000 ft/min or

10.2 m/s). Using Equation (2.4), vih = 12.3 m/s and later work will show that under these conditions vi = 0.7vih = 8.6 m/s. If the blade tip is considered then V = )R = 227.5 m/s whereas including the vertical component gives V = 228.3 m/s. Thus in this case
the standard approximation underestimates the total velocity by only 0.3%. Now the blade section incidence, a, will depend on its radial position, r, and from Fig. 2.3 for any spanwise position r:

a(r) = 0(r) — ф(г)

Using small angle approximations:

a(r) = 0(r) — = 0(r) — I(r)

This local incidence will lead to elemental lift and drag:

8L =1 p V1SCL = 2 p )2r2c(r)aa(r)8r

SD =1 p V 2SCd = 2 p )2r2c(r) CD(r)8r

which, from Fig. 2.3, can be combined to give elemental thrust and torque. Assuming the inflow angle is small and the lift/drag ratio is large leads to:

8T = b8L

8Q = b^8L + SD)r

The elementary power, 8P, required to produce the elementary thrust can be found from the elementary torque:

8P = )8Q = b Q^8L + 8D)r = )г(Ф8Т + b8D) = (Vc + v, )8T + )rb8D If this elemental equation is integrated along the rotor blade:

P = (Vc + v, )T + 2 p Q3b |c(r)r3CD dr (2.5)

Equation (2.5) is similar to the result obtained by adopting momentum theory except that we now have an extra term in the expression that represents the profile power required to keep the rotor turning against the torque produced by the profile drag. The total rotor thrust, torque and power can be obtained by integrating analytically the expressions for 8T, 8Q and 8P over the span of the blade. For a rectangular blade at constant pitch, where CD is now the mean profile drag coefficient for whole rotor, then:

T=1 pabV R (5—I)

Q = T ^ + 8 pbcVT R2Cd> (2.6)

P = T(Vc — v,) + 8 pbcVTrcd,