Blade stall and drag divergence

The high subsonic Mach numbers and high angles of attack experienced by rotor blades cause reductions in lifting performance (stall) and increases in drag (drag divergence). As both these effects cause an increase in the power required by a rotor they are typically included as additions to the power coefficients already determined. Although the variation of angle of attack and Mach number around the azimuth of a rotor in horizontal flight is complex these additional coefficients are calculated by assuming that drag divergence is most significant at ^ = 90° and blade stall at ^ = 270°. Estimation of the power increment due to compressibility (CPm) begins by determining the tip Mach number at ^ = 90° (M90). This Mach number is then compared with the

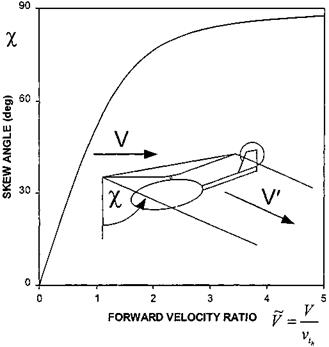
Fig. 2.15 Variation of main rotor skew angle with forward speed.

drag divergence Mach number that is itself dependent on the local angle of attack (a9C)). Thus after Gessow and Crim [2.19]:

CPm = 40.012 *Md + 0.1(*Md )3 ]

where:

*Md = M90 – Md – 0.06

and, as an example, from Prouty [2.6] for NACA 0012:

Md = 0.726 – 2.45«90

The local angle of attack is found by combining collective pitch (0C), blade twist (9T), longitudinal cyclic pitch (B1) and an inflow angle obtained from the mean induced velocity (vi0) [2.4]:

X

a90 = 90 + 9T + B1 + "j

1 – h

The increment in power coefficient due to retreating blade stall (CPs) is handled by assuming that the stalled region is diamond-shaped and centred about ^ = 270°. Within this region the section profile drag coefficient is taken to increase by 0.08 (for a NACA 0012 section). Hence, from Castles and New [2.20]:

cPs = 4z (1 – h2 )(1- X) V1 – X 2

where Xs is the dimensionless radius beyond which blade stall is present. This radius can be found by setting the general equation for angle of attack along the radial at ^ = 270° equal to amax [2.4 and 2.21]:

X

^max = 00 + XS0T — B1 + TP

Xs — p

Although amax varies with Mach number it is often sufficiently accurate to use the angle of attack above which low speed separation occurs (12.5° for a NACA 0012 section [2.21]). A correction to CPs is included if an unstalled section at the retreating tip bounds the stalled region.