Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
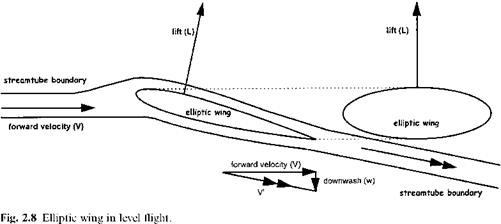
Elliptically loaded wing analogy
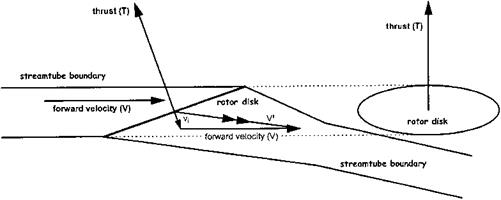
The analogy with an elliptically loaded wing, suggested by Glauert, provides us with a relationship for thrust. From Fig. 2.8 it can be seen that a lifting wing imparts a downwash velocity, w, on the flow as it passes over the aerofoil. If the wing is elliptically loaded then its effect on the air will be the same as a rotor with uniform inflow, (Fig. 2.9). Induced power, Pi, equals Tvi; since the rotor is assumed to act like a wing, Pi is considered to be the power required in overcoming the induced drag. Thus:
1
P = Tvi = V Di = 2 P^(V @ )3CDi
|
|
|
Fig. 2.9 Momentum disk in level flight. |
 |
 |
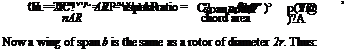But for an elliptically loaded wing (after McCormick [2.12]):
and so:
T = 2pAV’v1 (2.10)
Equation (2.10) provides the means to calculate the induced velocity in horizontal flight since T and V’ can be estimated from Fig. 2.8 and by considering the forces on the helicopter. The power required to drive the helicopter (PIDEAL) can be determined, as before, from the product of the thrust and the axial component of the relative speed of flow through the disk. Thus, the ideal power is given by:
pIDEAL=T (V sin у + v) (2.11)
