Frame Positioning

Let A and В be two frames containing three noncollinear points А і, A2, A3 and B, B2, B3, respectively (see Fig. 3.1). The position of frame В wrt frame A is determined by three displacement vectors Sb, a,, і = 1, 2, 3. Six of the nine vector coordinates are independent, i. e., a frame has six DoF. Are you surprised to encounter six rather than three degrees of freedom in the Euclidean three-space? Frames have the property of location and orientation, whereas space has only the attribute of location. That explains the difference. I will define these frame properties in more detail.

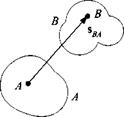
3.1.1.1 Location of a frame. Let A and В be two points of frames A and B, respectively (see Fig. 3.2). The displacement vector sba determines the location of frame В relative to frame A. We call the two points base points. A displacement vector can only relate to one point in each frame. It fixes the location of the base point, but leaves the frame the freedom of orientation. Yet remember that the frame points are mutually unchanging. Two more noncollinear and nonplanar points would define the complete location and orientation of the frame В wrt frame A. However, we chose three additional points such that they form the endpoints of an orthonormal vector triad and thus define the orientation of a frame.

3.1.1.2 Orientation of a frame. Build a triad from a set of three orthonor­mal base vectors (see Fig. 3.3):

a, яг, Я3 where я, a, = | j for) = j ; * = 1 > 2, 3; j = 1, 2, 3

with magnitudes one, which connect the base point A with three other points of a frame A. The orientation of a frame is given by this triad.

Just like location requires a reference point, so orientation needs a reference frame. A displacement vector models location, whereas orientation, as we shall see in Sec. 4.1, is portrayed by the rotation tensor. Both, location and orientation determine the position of a frame. A triad, with its base point and three vectors, is sufficient to define a frame.

You may interject that in Fig. 3.3 you recognize the familiar coordinate axes system. But not so! A triad is a physical entity, consisting of points and vectors, and is not a coordinate system. However, now we can finally bridge the gap. Among the coordinate systems associated with each frame, there is a particular one that coordinates the base vectors in the simple form [a i]A = [1 0 0], [«г]’4 = |0 1 0], and І аз ]д = [0 0 1]. It is called the preferred coordinate system and is the most important one among all the possible coordinate systems associated with a frame.