NON-DIMENSIONAL COEFFICIENTS

Before examining how the realism of the theories introduced above might be improved, it is necessary to discuss the concept of non-dimensional coefficients. These coefficients are analogous to the lift and drag coefficients that are a common feature of aerodynam­ics. Rather than lift and drag, in the case of rotorcraft, coefficients of thrust (CT), torque (Cq) and power (CP) are used. These coefficients are defined as:

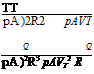CT =

CQ =

Note that power coefficient is numerically equal to torque coefficient (though, of course, they are different physically). Now converting Equation (2.7) into coefficient terms gives:

ct=2 abf u 9o+4 9i-1 *

CT = 2 as (3 90 +191 -1 *

where s is defined as the solidity of the disk that is the ratio of total blade area to disk area. Hence for a rotor with rectangular blades s = bcR I A. The relationship for thrust

CT ‘s 7 0O + л 01 T *

– 2 *

CT — 2 sa 3 0O.75 — 2 *

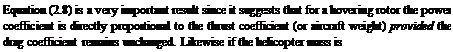coefficient can be simplified by altering the definition of blade pitch from the blade root to a position at three-quarter radius (60.75), since:

fixed and the rotor profile drag coefficient is constant then the power required to drive the rotor will vary as )3 so that CP will remain unchanged. This simple rule forms the basis of hover performance testing and is illustrated in Fig. 2.4.