Applications of Advanced Computational Methods

14.10.1 Unsteady Airfoil Performance

While unsteady aerodynamic effects are intrinsic to the helicopter, there are two unsteady airfoil problems that have received much more attention than others from a mod­eling perspective. These are blade vortex interaction (BVI) and dynamic stall. Both prob­lems are a particularly large source of unsteady airloads and are very difficult to predict. While BVI is a source of both unsteady airloads and very obtrusive noise (see Sec­tion 8.19), its occurrence does not limit the capabilities of the rotor system. As discussed in Chapter 9, the occurrence of dynamic stall, however, can limit both forward flight and maneuver capabilities of helicopters and is a more serious problem from a rotor airloads perspective.

Blade Vortex Interactions (BVI)

The 2-D BVI problem, as previously shown schematically in Fig. 8.36, has been widely addressed using CFD approaches, for example, see McCroskey & Goorjian (1983), McCroskey (1985), McCroskey & Baeder (1985), Singh & Baeder (1996), and Lee & Baeder (2002). While convecting past an airfoil, a vortex of positive circulation produces a downwash velocity while upstream of the blade (airfoil), and this changes to an upwash as it moves downstream. This situation leads to a rapidly and continuously changing angle of attack, resulting in highly unsteady aerodynamic loads – see Section 8.16.4 for an analysis of the problem using linear unsteady airfoil theory. The BVI problem usually requires compressibility effects in the flow to be accounted for if the correct amplitude and phasing of the airloads is to be calculated. In some cases, such as near the tip of the blade, the flow may be transonic. In this case the BVI problem is inherently nonlinear and quantitative prediction of the airloads requires advanced, nonlinear CFD methods for proper solution.

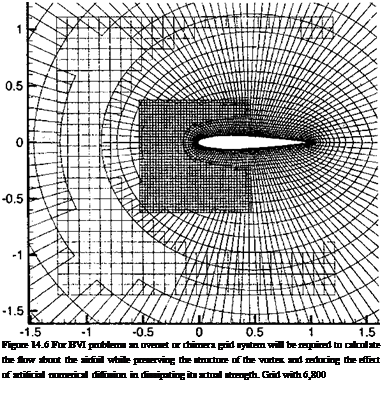
A problem that arises in such CFD solutions, however, is the need to preserve the physical strength of the vortex for relatively long times before and after its interaction with the blade or airfoil. This has been done relatively successfully using adaptive or chimera-type overset grids, such as in the example shown in Fig. 14.6. In this example, an О-type grid is wrapped around the airfoil and two overset H-grids are moved relative to the О-grid, tracking the vortex as it passes by the airfoil. The finer resolution of the flow afforded by the overset grids acts to reduce the numerical errors in the region of strong velocity and pressure gradient surrounding the vortex, and thus helps to reduce artificial numerical diffusion of the vortex during its interaction with the airfoil.

Figure 14.7 shows the complexity of the flow during a BVI event where shock waves are present in the flow. This might be the case, for instance, if the BVIs are encountered on the advancing blade at high forward flight speeds. The flow is calculated using an Euler CFD-basea approach with a chimera-type overlapping grid – see Lee & Baeder (2002). The vortex is initially well upstream of the airfoil and the flow about the airfoil is benign, except of course for the presence of the upper and lower surface shocks. As the vortex approaches the airfoil, rapid changes occur as the induced velocity field from the vortex alters the AoA of the airfoil and its pressure distribution. In this case the vortex passes about 0.125 chord lengths below the airfoil, so the interaction is relatively strong. Notice the effect of the vortex on the lower surface shock wave – as the vortex passes by the shock bifurcates, adopting a lambda shape for a short period before returning to its original geometry. Amazingly, despite the high pressure gradients in the flow at and near the shock wave, the vortex emerges from the interaction with the airfoil and the shock wave in a

Lee & Baeder (2002) and courtesy of Yik-Loon Lee.

relatively undisturbed form. According to Fig. 14.7(d) the vortex does, however, appear to lose its initial radially symmetric form.

Of course, the prediction of BVI in 3-D viscous flow and over the entire rotor is the ultimate goal for CFD methods. This is, however, an extremely ambitious task, requiring high-resolution calculations using many tens or hundreds of millions of grid points. One outstanding issue is how to capture 3-D vortical flows accurately using 3-D overset grids. Grid refinement continues to be limited by computer memory and speed, and it would seem that approaches based on indefinite grid refinement will probably not be that useful in the shorter term. As is clear from the foregoing 2-D example, overlapping grids offer a very powerful and natural approach to solving the flows found on the various stationary and moving vcomponents of helicopters, however. The alternative of regenerating the grid at every time step, change in flight condition, or whatever, is expensive and prohibitively time consuming. A combination of refinement and proper placement of overset grids (say, for example, using the FVM or VTM as guidance) would be a very powerful technique if properly developed, and this is a promising area for further research.