Boundary Layer Equations
At the Reynolds numbers typical of helicopters, the viscous terms in the Navier – Stokes equations are significant only in a thin shear layer, called the boundary layer, near the surface of the vehicle. To model the flow in this layer, a simplified subset of the Navier – Stokes equations can be derived that exploits the fact that the length-scale of the variation of the flow variables is very much smaller normal to the surface than parallel to the surface.
The chief advantage of the boundary layer approach is that it allows an inviscid “outer” solution (calculated for instance using the Euler equations or a potential flow solver) to be modified for the effects of viscosity near the surface of the rotors and fuselage. This approach leads to a class of numerical techniques known as zonal or viscous-inviscid interaction methods. Such methods have proved very useful in airfoil design, but can also be useful
in predicting rotor and airframe loads on helicopters. The basic principle is first to solve the inviscid flow problem and then to solve the boundary layer equations. The inviscid solution is then repeated after applying a correction to take into account the effect of the finite thickness of the boundary layer on the outer flow. The resulting solution thus yields, to first order, a high Reynolds number solution to the Navier-Stokes equations. Care must be taken, though, where grossly separated flows are encountered, for instance, in the lee of bluff fuselages and cowlings, because under these conditions the basic assumptions of the boundary layer approach are invalidated.
Consider the situation in two dimensions. If x is in the direction parallel to the surface and у is normal to the surface, then, as the Reynolds number of the flow becomes very large, the Navier-Stokes equations for an incompressible flow reduce to
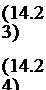 3 и dv
3 и dv
—— 1— =0 (continuity),
ox dy
3и ди 1 dp 32u
и ——-v— =———— b v—- (^-component of momentum),
Эх oy p ox dy1
![]() (pressure gradient normal to surface)
(pressure gradient normal to surface)
because the gradients of the fluid properties in the x direction become much smaller than the gradients in the у direction. If the flow is unsteady, then the momentum equation
![]()
 |
3 и ди ди 1 dp д2и
— – b и— – J – v— =—————– Ь v——
31 дх 3у р дх 3у2
should be used instead. At the edge of the boundary layer у = 8, where 8 is the boundary layer thickness [which by definition is where the local velocity approaches 99% of the external flow (or edge) velocity, Ue(x, t) – see Section 7.3.2]. Because the pressure across
the boundary layer (i. e., normal to the surface) is constant (Eq. 14.25), the pressure at any point on the surface is taken to be the pressure just outside the boundary layer. The momentum equation outside the boundary layer can thus be rewritten as
![]() dUe dUe = 1 dp
dUe dUe = 1 dp
31 e dx p dx
Using this equation, the pressure can be eliminated from the problem and the momentum equation within the boundary layer becomes
Associated with the solution of the boundary layer equations is the concept of a displacement thickness, 3*, which is written as
![]() ‘-/Л’-*)*-
‘-/Л’-*)*-
![]()
![]() The displacement thickness is a measure of the extent to which, if the effects of the boundary layer are to be included in an inviscid model of the flow away from the surface, the shape of the surface might be displaced away from the original surface to yield the same flow rate as in the viscous flow with the boundary layer present. This is same as saying that the external, inviscid, flow about the body can be obtained by solving the equations about a shape that is generated by adding the displacement thickness to the actual shape of the body. This type of approach is an example of a so-called weak interaction method. Although obviously still an approximation, and apart from the restrictions on the method mentioned above, this approach yields more representative flow solutions at the Reynolds numbers appropriate to helicopters than if the viscous effects were completely ignored in the calculation.
The displacement thickness is a measure of the extent to which, if the effects of the boundary layer are to be included in an inviscid model of the flow away from the surface, the shape of the surface might be displaced away from the original surface to yield the same flow rate as in the viscous flow with the boundary layer present. This is same as saying that the external, inviscid, flow about the body can be obtained by solving the equations about a shape that is generated by adding the displacement thickness to the actual shape of the body. This type of approach is an example of a so-called weak interaction method. Although obviously still an approximation, and apart from the restrictions on the method mentioned above, this approach yields more representative flow solutions at the Reynolds numbers appropriate to helicopters than if the viscous effects were completely ignored in the calculation.
![]() In many engineering problems the details of the flow inside the boundary layer are of no interest and only the effects of the boundary layer are needed. For example, the shear stress on the surface (to estimate the viscous drag) and the boundary layer displacement thickness (to perform a correction to the external flow) might be required. These variables can be calculated directly from an integrated form of the boundary layer equations, called the momentum integral equation, usually attributed to von Karman (1921). In this case the governing equation is
In many engineering problems the details of the flow inside the boundary layer are of no interest and only the effects of the boundary layer are needed. For example, the shear stress on the surface (to estimate the viscous drag) and the boundary layer displacement thickness (to perform a correction to the external flow) might be required. These variables can be calculated directly from an integrated form of the boundary layer equations, called the momentum integral equation, usually attributed to von Karman (1921). In this case the governing equation is
d<) d Hp Tim
—{U2e0) + 8*Ue —- = —, (14.30)
dx dx p
where tw is the shear stress on the wall (surface) and
/ и / і/
e=!Al~tAt)dy – <1431)
is the so-called momentum thickness. This equation is very general because no assumption is made about the relationship between zw and the velocity gradient, and so the equation can apply to both laminar or turbulent boundary layer flows. After choosing a suitable form for the velocity profile across the boundary layer, the momentum integral equation can be solved to find the key variables describing the properties of the layer (i. e., 8, 8*, 0, and xw). While in some cases solutions to the momentum integral equation can be found in closed form, in most cases numerical solutions must be obtained. See Houghton & Carpenter
(1993)
or Katz & Plotkin (1991) for a survey of the various possible approaches.














