Factors affecting range performance

Consider now the change in power required as weight is increased at constant true airspeed, V. The rotor thrust, T, must rise correspondingly and this will cause an increase in the inflow velocity, vi. In addition, if the higher collective setting required at higher AUM leads to increases in drag due to Mach effects (reducing Mcrit) then CD will rise above its nominal value. Therefore the power required must increase with weight and consequently the SAR will reduce. So:

SAR ё W

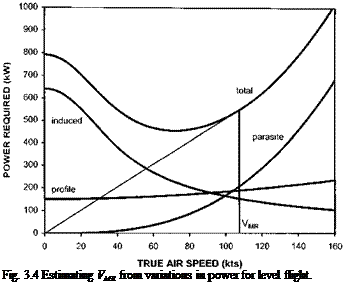
Alternatively, consider the variation of power required with true airspeed for a given weight. At a fixed weight the thrust required will be approximately constant assuming a modest parasite drag coefficient. Therefore the induced velocity will reduce as airspeed increases whereas the parasite power increases rapidly and the profile power increases but at a more gentle rate. Consequently the overall trend in the total power required is the familiar U-shaped curve. This curve can be used to determine the speed for best range (VMR) since a line drawn from the origin to a point on the curve is proportional to PIV. Therefore the lowest P/V (highest SAR) will occur at the point where the line is tangential to the curve, see Fig. 3.4.

It is instructive to determine the factors that affect VMR. Typically the maximum range speed will be in the moderate to high forward speed bracket so the high-speed approximation may be used:

— vh — W

V — V — 2pAV

Thus the total power required can be written as:

W2 1 1

P — 1.22PAV + 2 P V 3f + 8 pbcRV3 (1 + 4.3ц2 )CD

Now maximum SAR will occur at the speed at which P/ V is a minimum, that is when:

A P

dV V

If it is assumed that the profile drag is approximately constant with speed then:

Then:

VMR ё VW

So the speed for best range, assuming SFC and profile drag is approximately constant, will be proportional to JW