Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Flying at best range speed
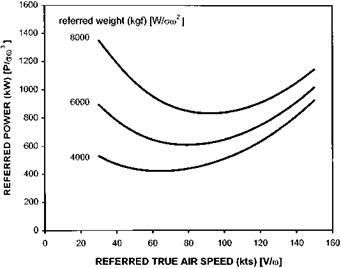
Figure 3.5 shows typical curves of referred power (P/am3) against referred TAS (V/m). Assuming constant specific fuel consumption and ignoring the effects of referred RRPM (m/J0), this figure can be used to determine the ranges of altitude, RRPM and TAS that will ensure maximum SAR at any weight. Since SFC is constant then SAR will be directly proportional to V/P.
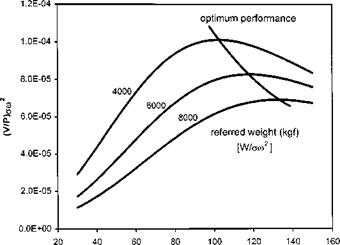
If referred TAS is divided by referred power then a trend that indicates the variation of SAR with referred weight (W/am2) can be produced, as shown in Fig. 3.6. From
|
Fig. 3.5 Variation of referred power with referred weight and TAS. |
|
REFERRED TRUE AIR SPEED (kts) [V/m] Fig. 3.6 Variation of referred SAR function with referred weight and TAS. |
this figure it is possible to determine the optimum value of Varn2 /P and the referred TAS at which it occurs for each referred weight.
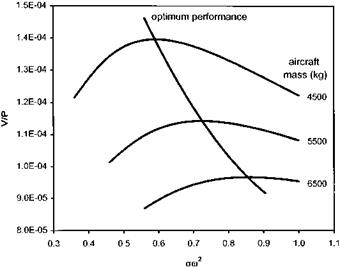
Suppose the flight conditions required to ensure maximum range at an actual aircraft mass of, say, 5500 kg are to be determined. The pilot can change airspeed, NR and altitude (relative density) therefore the variation of V/P with am2 must be evaluated. Using the optimum Vam2/P and Wlam2 data obtained from Fig. 3.6 it is
|
Fig. 3.7 Variation of SAR function with referred weight and TAS. |
possible to plot the variation of V/P with am2 for a particular mass, see Fig. 3.7. This figure shows that, for a given weight, there is a unique value of am2 which will give the highest V/P and the best range performance. In other words, for each actual weight there will be a unique referred weight (Wlam2) or CT which will give the best range performance. The practical outcome of this situation is that to ensure maximum SAR the pilot must change altitude as fuel is burnt and adjust rotor speed to suit the prevailing ambient conditions.
Consider the choice of range TAS. From Fig. 3.6 the variation of V/m, for best range, with Wlam2 can be determined. This relationship can be used to select the TAS for each actual weight as density altitude is increased using practical rotor speeds. In this way even though the range performance may be sub-optimal due to power-on RRPM considerations the most appropriate range speed is being used. However, if airspeed limitations, perhaps due to airframe or rotorhead stresses, are introduced it can be seen that the range performance may be further reduced by the inability to fly at a high enough TAS, see Fig. 3.8.
The combined effect on VIP (or SAR) of imposing power-on RRPM and TAS limits is also shown in Fig. 3.9. It can be seen from this figure that the optimum range performance is only achieved at low weight and high density altitude, or at high weight and low density altitude. Nonetheless, even when flying optimally at high weight the actual SAR will be lower than that recorded at lower weights.
