Maximum Flight Speed for a Propeller-Driven Aircraft
To find the maximum speed for the propeller-driven Messerschmitt fighter, we follow a procedure similar to that described previously for jet-propelled vehicles. To do this, it is necessary to determine the actual power available for producing thrust. This power can be estimated by reducing the rated power (sometimes called the shaft brake horsepower) by a factor that considers the aerodynamic losses of the propeller. The power available can be written as:
PA = power available = nPRated, (9.16)
where n is the propeller efficiency. A typical value for a good propeller design is on the order of n = 0.88, which was used in the estimated power available shown in Fig. 9.5. There usually is a correction to account for the effects of altitude on engine performance, but this is not indicated in the Figure. The usually significant PA variation with speed also is not represented properly. To graphically find the maximum speed, we locate the point where the power available is equal to the power required. For the case shown, the maximum speed at altitude is about 379 mph (610 km/hr), which is in good agreement with the values shown in Table 9.1. Due to the higher power required at the lower altitude, the maximum speed is reduced, so that at sea level, the Bf-109G is limited to a top speed of about 300 mph (482 km/hr). These
|
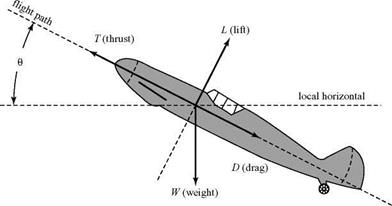
Figure 9.6. Airplane in steady climb. |
numbers are in good agreement with published data for this airplane. In working with the power equations, recall that:
1 horsepower = 550 f lbf = 746 watts.
sec