Maximum Range of a Subsonic Airplane
We complete this brief set of applications of basic aerodynamics by estimating the range of a propeller-driven aircraft. The key here is to introduce the rate at which fuel is used by the propulsion system and to use it in determining the rate at which
the weight of an airplane changes with distance. We define the specific fuel consumption, c, as:
dwf
![]()
 |
dt _ weight of fuel consumed per unit time Prated rated engine power output
where the power, Prated, represents the brake-horsepower rating of the engine. From this, we see that the weight of an airplane changes at the same rate as fuel is consumed so that the weight change per unit time is:
d – = – c P„„d, (9-25)
where W(t) represents the aircraft weight. The negative sign is inserted to emphasize that W decreases as fuel is consumed. Working with the differential form of Eq. 9.25, we see that the length of time required for a weight change, dW, is:
and, assuming constant flight speed, the corresponding distance traveled is:
![]() ds = Vdt _- VdW
ds = Vdt _- VdW
cPrated
To find the range, we integrate this expression over the weight change from the initial (full tanks) to the final (empty tanks) condition. Thus, the range, K, is found from:
R Wf
K_[ds = – [ (9.28)
J J cP
0 Wi cPrated
To simplify the problem, we neglect changes in speed and rate of fuel consumption in initial takeoff and climb to cruising altitude, the effects of wind and atmospheric disturbances, and changes in power settings at the end of the flight. We note that in level, unaccelerated flight the power required and power available are equal and that:
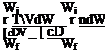 |
||
Then, the range equation becomes:
The last series of changes involves multiplying the top and bottom of the integrand by the weight and then replacing the weight in the numerator by the lift because they are equal in level, unaccelerated flight. If it is reasonably assumed that the parameters c, n, and L/D remain constant during flight, then Eq. 9.30 can be integrated to give the final formula for range:
![]() (9.31)
(9.31)
the famous Breguet range equation mentioned in Chapter 1. This was introduced previously to demonstrate the importance of the aerodynamic efficiency in the operation of an airplane. To achieve great range, it is necessary to start with a large mass ratio, as represented by the logarithmic term. This ratio depends on how much fuel can be carried and how efficiently the airplane structure was designed so that its weight is as low as possible. The need for an efficient propeller is illustrated by the direct dependence on p. Finally, there is no question that the L/D ratio must be as large as possible. These ideas were used by Charles Lindbergh in his 1927 flight from New York to Paris in the Ryan Spirit of St. Louis, using the best technology of the time. Material limitations precluded his use of high AR wings, as used in the more recent Voyager around-the-world flight to obtain the best possible L/D ratio. The necessary range for the Spirit was achieved mainly by accommodating the necessary amount of fuel in a relatively light airframe.
To illustrate the use of the Breguet equation, we use it to estimate the range of the Ryan Spirit of St. Louis. This aircraft took off from New York in the spring of 1927 carrying 450 gallons of fuel (weighing 2,750 lbf). The initial gross weight was 5,250 lbf. The best L/D ratio was about L/D = 9.8 (considerably less than the more modern Bf-109G design). The specific fuel consumption of the 220-hp Wright Whirlwind (J-5C) engine at 200 hp was:
c = 0.53 lbf/hr/hp,
so that assuming a propeller efficiency of n = 0.82 and a cruising flight at a throttle setting producing 200 hp, the range is given by:
= 2.23.107ft = 4,220 miles,
which is comparable to published values for this aircraft. Examine this calculation to see how the units are adjusted in the specific fuel consumption to give the range in feet. The result is divided by 5,280 ft/mile to determine the range in statute miles.












