Navier-Stokes Equations

Many of the aerodynamic problems found on helicopters involve viscous effects and the generation of turbulence. These effects are important in the 3-D turbulent boundary layers found on the blades and airframe, unsteady flow separation and dynamic stall, the formation and subsequent structure of the blade tip vortices in the rotor wake, as well as in a host of rotor-airframe interaction phenomena. All of these problems have been alluded to in previous chapters.

The Navier-Stokes equations are the fundamental equations governing the fluid dynam­ics of the helicopter system. They encompass the principles of the conservation of mass, and momentum and energy interchange within a fluid. For a perfect fluid in three dimensions they can be written in a Cartesian, nonaccelerating coordinate system as

(Mass conservation),

dp dzi ;

———— і—— — (Momentum interchange),

dxj dxj

with p as the flow density, u — щ, where і — 1,2, 3, being the velocity vector, p is the pressure, h as the specific enthalpy, r,-j is the stress tensor, and q = qt, where і = 1, 2, 3, as the heat flux vector. The ideal-gas equation of state is usually used to relate the thermo­dynamic quantities using

p — pRT and h = CpT,

where R is the gas constant, Cp is the specific heat at a constant pressure and T is temperature. The heat flux is usually given by the equation

dT

4i = (14-5)

dxj

where к is the thermal conductivity of the fluid. Finally, the flow about the helicopter is invariably approximated as an isotropic Newtonian fluid, for which the relationship between stress and strain is given by

where Sij is the Kronecker delta function ($,-j = 1 for і = j and Stj = 0 otherwise) and p, is the coefficient of dynamic viscosity.

For practical use, the Navier-Stokes equations are usually rewritten in so-called conser­vation form (compared to the tensor differential form given above), that is, in the form

9Q ЭЕ 9F 9G

— _l_ — — _|

dt dx dy dz

where Q is the conserved variable vector and E, F, and G are expressions, called the flux vectors, giving the rate at which mass, momentum, and energy are being transported at any
point in the flow. This latter equation is often expanded into a form with the viscous terms on the right-hand side to give

9Q ЭЕ 3F aG _ 3EV 3FV dGy

dt dx dy 3z 3jc dy dz

where Ev, Fv, and Gv are the fluxes resulting from the viscosity of the flow. This form allows a reduction to the so-called thin-layer Navier-Stokes equations where the viscous derivatives with respect to the downstream and spanwise direction are neglected to give the form

3Q ЭЕ 3F 3G _ 3S

dt dx 3y dz dz ’

for a suitably defined viscous flux, S. A further reduction can be made by adopting a mathematical model for the turbulent contribution to the viscous fluxes in terms of the mean flow properties. In this form they are called the Reynolds averaged Navier-Stokes or R ANS equations, and this form is used by many industrial strength computer codes.

It should be apparent that the Navier-Stokes equations are a set of strongly coupled, highly nonlinear partial differential equations. This means that they cannot usually be solved without making major simplifying assumptions. The most common practical simplification is to avoid the treatment of turbulent mixing and the associated viscous shearing effects by assuming a laminar flow. This greatly simplifies the solution of the Navier-Stokes equations, but it should be borne in mind that even at the lowest Reynolds numbers found on helicopters, the flow is turbulent. The need to model turbulence requires the introduction of empirical closure models, of which many types have been developed – see, for example, the popular models devised by Baldwin & Lomax (1978) and Spalart & Allmaras (1992). Resolution of the turbulence scales requires extremely fine grids v/ith fine numerical discretization, and hence large amounts of memory and the fastest computers. Calculation of turbulence is difficult enough for even the simplest of flows and is certainly not yet practical for a complete helicopter. Nevertheless, solution of the Navier-Stokes equations will eventually be required for a full understanding of helicopter aerodynamics, even though practical use of these equations in the engineering design of new rotors and helicopters still lies a long way in the future.

There have been many algorithmic developments in the numerical solution of the Navier-Stokes equations. The fundamentals and historical development are summarized by Caradonna (1990), who also describes the various forms of the equations that are re­quired for the analysis of various classes of helicopter problems. A key issue in any problem is the generation of the grid structure on which to solve the governing equations. Unlike a fixed-wing aircraft, a helicopter rotor induces significant velocities at large distances from itself. This means that the size of the computational domain, which should be as small as possible for economy, needs to be much larger than for corresponding fixed-wing problems if the possibilities of artificial flow recirculation and other nonphysical problems within the computational domain are to be avoided. This makes computer memory requirements very large indeed.

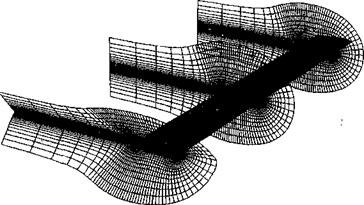
For most helicopter applications the Navier-Stokes equations are solved on a grid that rotates with the blades, an example being shown in Fig. 14.1. This requires a transformation to put the equations into a coordinate system that is stationary relative to the rotating hub. This transformation eases the problem of generating the grids used to calculate the flow about the blades, but introduces additional terms into the equations (to account for the acceleration of the coordinate system) that can destabilize the numerical method if not properly treated.

Figure 14.1 Example of the gridding of a helicopter rotor blade using C-type grids on which to solve the Navier-Stokes equations. Source: Grid courtesy of Karthikeyan Duraisamy.

Several types of grid systems are appropriate for analyzing various parts of the helicopter flow problem. Grids are categorized according to their geometric shape, that is, О-, C-, and H-type grids. The O – and C-type grids are often used for analyzing the flows about blades as they can be made to conform to the curved airfoil shape of the blade surface. H-type grids are sometimes used instead, as they allow a compromise between the advantages of a simple Cartesian grid geometry and an ability to refine the grid near the surface of the blade. Overset or chimera grid systems are locally refined grids that are superimposed upon a main (background) grid. These are useful in helping to resolve local flow phenomena without the need to grid the entire flow domain at high resolution. They can also be used to resolve the difficulties in dealing with a domain that is most easily meshed using separate grids that can move relative to each other. Interpolation routines are required to transfer information between the overset grids in the flow solver, and the accuracy of these procedures needs to be carefully controlled to avoid degrading the overall accuracy of the numerical solution. Structured grids such as these, though, can be very labor intensive to create. Unstructured grids, composed of irregularly distributed tetrahedral elements, are increasingly being used because these have the advantage that semi-automatic mesh generation software can be used to create this type of grid around very complex surface geometries.

The numerical technique used to solve the Navier-Stokes equations may be based on either a finite-difference or a finite-volume approach, and numerous algorithms have been developed, each with their own particular advantages. Finite-difference methods approxi­mate the various space derivatives in the equations using expressions based on Taylor series approximations at each node on the computational grid. (A node can be considered as the intersection between grid lines.) Finite volume methods operate on an integral form of the Navier-Stokes equations, derived from Eq. 14.7, and treat the computational domain as a patchwork of cells rather than nodes. The integral of the mass, momentum, and energy within each cell is divided by the cell volume to get an average conserved variable and average fluxes are derived in a similar way by integrating over the boundary of the cell. Although there are many good computational reasons to adopt a finite-volume rather than a finite-difference approach, both approaches are ultimately equivalent in the mathematical sense. However, finite-difference methods can only operate on structured grids, whereas finite-volume methods can be used on both structured and unstructured grids.

Some of the first approaches to solving the Navier-Stokes equations (RANS equations), in this case for a rotor, are described by Agarwal & Deese (1988) and Wake & Sankar (1989). The effect of the rotor wake was computed by means of a vortex method and cou­pled to the Navier-Stokes solution for the blade flow by means of a correction to the AoA along the blades. This is the essence of the so-called loose or “weak” coupling procedure (see page 806). Many variations of this basic approach have followed this. One particu­larly promising modem Navier-Stokes approach for helicopter applications is called the Transonic Unsteady Rotor Navier-Stokes (TURNS) method – see Srinivasan & Baeder and colleagues (1.992,1993). More modem methods use a strong coupling approach where both the rotor and the wake flow are solved simultaneously. In the latest versions of this RANS-type method, a high-order discretization of the governing equations is used to limit the extent of the nonphysical numerical dissipation that is a well-known but very undesir­able feature of finite-difference or finite-volume solutions to the Navier-Stokes equations. Another, similar method thaf has been used for helicopter applications is OVERFLOW, which is based on a general purpose Navier-Stokes code developed by NASA – see Chan et al. (2001) for an overview.

In these approaches, the rotor blades and computational domain are usually enveloped in body conforming grids, an example of which has been shown in Fig. 14.1. Here a rotor blade has been enveloped in a C-type grid to allow good resolution of the flow near the blade surface and in the wake downstream of the blade. Ail types of CFD methods solve the governing fluid dynamic equations to an accuracy that is dependent on the resolution of the grid, and Navier-Stokes calculations require these grids to be created to give extremely fine resolution of the flow near the blades and/or body surfaces (and in the wake downstream) where the viscous stresses are the highest.