Newton’s Second Law

Newton’s second law is the most important tool for modeling aerospace vehicle dynamics. It governs the motions of the c. m. of the vehicle subjected to external forces. We apply it first to a single particle and then to a collection of particles and eventually arrive at a form that is most suitable for our modeling tasks.

For a particle i, Newton’s second law postulates

D’pj = ft (5.6)

The equation states that the time rate of change wrt the inertial frame / of the linear momentum of particle і wrt the inertial frame equals the force act­ing on the particle. Introduce the definition of linear momentum from Eq. (5.1),

pj — m, D’su, into the left side of Eq. (5.6) so that

D1 p – D1 (niiD1 Su) = rtiiD1 D1 su + D’iti^D’su

where the last term is zero because the mass of a particle is time invariant. Now we sum over all of the particles of body B. The internal forces will cancel because of Newton’s third law, but the external forces remain

Y^miDJDIsa = Ytfi (5.7)

І І

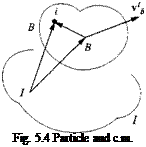
Let us introduce the c. m. В of the collection of particles (see Fig. 5.4)

Sir — SiB + $BI

and obtain

D’sw + J^miD’D’ssr = ^/;

І І І

With the mass of each particle constant, we can place it inside the rotational derivative and move the summation sign. Because В is the c. m. of all particles, the first term vanishes:

Abbreviating mi — mB and summing over all forces JT/j – = /> we arrive at Newton’s second law for body В relative to the inertial frame /:

mBDID, sBi = f (5.8)

Let us introduce the velocity v’B = D’sbi of the c. m. В wrt the inertial frame I. Newton’s law reads then as follows: The mass mB of body В times the inertial acceleration a’B — D! vlB of its c. m. В equals the resultant external force/.

mBDIv1B = f (5.9)

From this derivation we conclude that the c. m. В of a system of particles m, moves like a single particle В whose mass is the total mass mB, subject to the
force/. Notice that we did not invoke a rigid body assumption, although most of our applications will do so.

We have formulated Newton’s law in an invariant tensor form, which can be expressed in any allowable coordinate system. For instance, in coordinates ]7, associated with the inertial frame I, we get the ordinary time derivative

For a noninertial coordinate system, say ]B, associated with the body frame B, we transform the rotational time derivative to the В frame via the Euler transformation to get the ordinary time derivative in the ]B coordinates:

= [/]B

+mB[^lBIB[v, BB = [f]B

The acceleration [du^/dfj® is the inertial speed, coordinated in body axes, with its components subjected to the ordinary time derivative. The additional term [Г2й/|й[Т.’д]й is called the tangent acceleration.

As we developed our preferred formulation, Eq. (5.9), we assumed that the body holds onto all of its particles; in other words, the mass is time invariant. If particles are ejected, as for instance by a rocket motor, the linear momentum is changed, resulting in a thrust force. Traditionally, however, that force is moved to the right side of Newton’s law and considered an external force (see Example 5.6). On the left side the mass has become a function of time.

Example 5.2 Trajectory Equations

The translational equations of an aerospace vehicle are directly derived from Newton’s law, Eq. (5.9). With mB the mass of the vehicle, vi the linear velocity of the c. m. relative to the inertial frame /, and the external forces consisting of aerodynamic force fa, propulsive foreefp, and gravitational force mBg, the translational equations are

mBDlvIB = fa + fp + mBg

This tensor equation is valid in any allowable coordinate system. The simplest implementation is in the inertial coordinate system |;

m^v1^1 = [faY + [fp]1 + mB[g]7

However, the aerodynamic and propulsive forces are most likely given in body coordinates ]B and the gravitational acceleration in geographic coordinates ]G. With the two transformation matrices [T]B1 and [7’ |c/ we can formulate the dif­ferential equations for computer programming

= [f]BI[fa, P]B +mB[T]G,[g]G

where the aerodynamic and propulsive forces have been lumped together. To calcu­late the trajectory, another integration is necessary for obtaining the displacement vector sb/ of the vehicle c. m. relative to an inertial reference point I

D’sbj = vlB

In inertial coordinates

– [4]’ (5-П)

Equations (5.10) and (5.11) are the six differential equations that must be solved, starting from initial conditions, to generate the trajectory traces.

Example 5.3 Translating Inertial Frames

Problem. Newton’s first law states the experiential fact that, unless bodies are subjected to forces, they continue in a state of rest or uniform motion. From Newton’s second law, mBDIvlB = 0, indeed we conclude that the inertial velocity does not change. This statement reflects also on the characteristic of the inertial frame. Newton’s second law holds equally in an inertial frame at rest or at uniform motion in a straight line. Let us prove that fact.

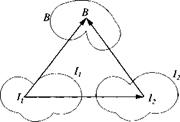
Solution. Figure 5.5 depicts the body В with c. m. В and two inertial frames 11 and I2 with two arbitrary reference points h and /2, respectively. The presup­position of both inertial frames not accelerating relative to each other implies that the mutual linear acceleration and angular velocity are zero:

DhDhshh= 0, fthI] =0 (5.12)

Introduce the vector triangle of Fig. 5.5

*B/i = SBI2 + SI211

into the left side of Newton’s second law, Eq. (5.8),

mBDhDhsBh= f (5.13)

and obtain

mBDhDhsBh+mBDI’Dhshh = f

The second term on the left-hand side vanishes because of the first premise of Eq. (5.12). The first term is modified twice by Euler’s transformation to the /2 frame, and the second premise of Eq. (5.12) is used

mBDI’DhsBh =mBD,'(DhsBh+nh,’sBi2) =mBDhDhsBh

= mBD,2(DhsBh)+mB£lhIi(Dl2sBl2) = mBDhDhsBh

Summarizing, from Eq. (5.13), with the assumptions of Eq. (5.12), we derived the alternate form

mBDhDhsBll = f

Both inertial reference frames lead to the same dynamic equation. Because either frame /1 or /2 is suitable, all inertial frames, not mutually accelerating, lead to the same formulation of Newton’s second law.

Example 5.4 Two-Body Problem

Problem. Given are two particles with masses m 1 and m2, located at B and B2 and subject to the external forces/j, f2 (see Fig. 5.6).

1) Determine the displacement vector sbi of the common c. m. В wrt an inertial reference point I. Express the location of the two masses s в, / and s в, / in terms of sbi and sb, b2-

2) Apply Newton’s second law to both masses individually and then show that (m 1 + ш2)/У D1 s в і =/, + /2 and explain what the meaning of this reduction is.

3) If the point masses are not subject to external forces, then /1 + /2 = 0. What motion does the common center of mass В execute?

4) Let m 1 be the mass of a satellite and m2 the Earth’s mass. Assuming m2»mi and neglecting the acceleration of the common mass center, give the simplified equation of motion of a satellite orbiting the Earth. Summarize the assumption for this simplified single body problem.

Solution. 1) From the vector triangle in Fig. 5.6, we get the first relationship

SBiB2 = «В,/ ~ SB2I

Because В is the c. m. of both particles, the second condition is (mi + m2)sBi = + m2sB2i

Solve both equations first for sBli (multiply the first by m2 and add both equations),

m2

®в1/=®вН—– ;—- sb1b2 (5.14)

mi + m2

and then similarly for sBl[,

m 1

вb2i ~ sbi——– ;—- Sfiib2 (5.15)

mi + m2

2) Apply Newton’s law to particles B and B2 and substitute Eqs. (5.14) and (5.15), respectively,

= m1DIDISBi+-— — – DIDISB1Bi = /1 m 1 + m2

rm&DhB^i = m2DlD’sBi – D! sB]b2 = f2

mi + m2

then add both equations

mD1 D’sB, = f, т = т{+т2, f-fi + f2

If В is the common c. m., then Newton’s law is applied as if all mass m = m 1 + m2 were concentrated at the c. m. and acted upon by the resultant force/ =fx + /2.

3) Without external forces Eq. (5.17) becomes

malB = mD1 D‘sB — 0

i. e., the acceleration of the common c. m. is zero.

4) When m2 » mi, from Eq. (5.16) we obtain

mDl DlsBl + mD! D1 s ВіВг = /, and if we assume that the common c. m. В is not accelerated,

miD’D’sBf^ = /1

The reduced single-body problem of a satellite B orbiting Earth B2 can be solved as if the common c. m. is centered in Earth’s c. m. B2. The assumptions are that 1) m2^> m and 2) the common c. m. is not under acceleration.

Example 5.5 Pulse Thruster

Problem. The thruster of a satellite increases with a single pulse the satellite speed from vo to Vf. The total particle count of the satellite is s, and the thruster ejects / number of particles at an exhaust velocity of ve. Assuming that the pulse is instantaneous, what is the increase of the satellite speed Av — 1if — v0l

Solution. Let us start with Eq. (5.6) and sum over all particles and recognize that no external forces are applied:

S+f

T, DlPf= 0

i=l

The total linear momentum is therefore conserved:

S+f

Pf = const

1=1

Divide the particles up into satellite and ejected mass:

s+f s s+f

E p’ = E p’ + E p! =const (5-i8>

/=1 / = 1 i=s–1

We reduce the problem to one dimension in inertial coordinates, label the satellite mass

ms = m,

i = l

and the mass of the ejected fuel

S+f

mF = m,

Before pulse firing, the linear momentum is (ms + mF)vo. The pulse is ejected in the opposite direction at — ve wrt the satellite and (—ve + Vq) wrt to the inertial frame. Afterward the satellite’s linear momentum is msVf and that of the fuel mF(vо — ve). Using Eq. (5.18) in one dimension delivers

(ms + mF)vо = msv/ + mh (vq — ve) = const

Solve for Vf

msv о + mFve

and the velocity increase is

The higher the exhaust speed ve or the fuel mass m /., then the greater the increase in satellite speed. What happens to the c. m. of the total particle count s + /?

Example 5.6 Rocket Propulsion

A rocket motor ejects fuel particles continuously. We regard Eq. (5.19) as the velocity increase per time interval At caused by the fuel mass expenditure of Am = mF with the total mass of the vehicle m = ms + Am ^ ms. If we formally take the time derivative of Eq. (5.19) and, recognizing that ve and ъу> are constant, we obtain

Av ve Am

Before we can write the thrust equation, we have to address a subtlety in sign change. In the previous example the fact that the linear momentum of the exhaust is opposite to that of the satellite was expressed by the negative sign of ve. Now, with the fuel loss derivative being negative, the exhaust velocity should be positive. Therefore, we change its sign and make the transition to differentials:

(5.20)

This is Oberth’s famous rocket equation, which can be solved by separation of variables:

Solving the integrals with ъу> and m0 as the initial values, the increase in speed An is

A v = v — Vo = veln— (5.21)

m

The rocket’s burnout velocity v increases with increasing mass fraction mo/m and exhaust velocity ve. In engineering applications, fuel flow is usually taken positive and the rocket thrust calculated from Eq. (5.20):

F — mve

Thus, we have demonstrated how the time rate of change of momentum of rocket propellant produces thrust. This force is moved to the right side of Newton’s equation and portrayed as an external force.

Newton’s second law suffices to model the trajectory of an aerospace vehicle. Deceptively simple to write down in inertial coordinates, it has many variants that become important for applications. We already encountered the formulation in body axis, which gives rise to the tangential acceleration term. Other variations consider noninertial reference frames and points that are displaced from the c. m. We consider such transformations next.