Problems of Chapter 10

Problem 10.1

In the frame of the reference-temperature concept the Reynolds number is defined as

which can be written as

p ______ poo ^OO % P poo _______ p P poo

р<ж р<ж p р<ж p

Because p = const. across the boundary layer and p ж Tw, we can for­mulate

P^Roo = (ТоА1+Ш Poo At* T* ) ‘

For the thickness of the Blasius boundary layer this leads to

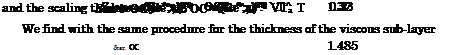
For the thickness of the ^-th-power turbulent boundary layer we obtain

Problem 10.2

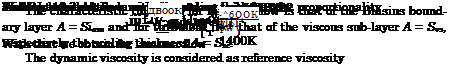We write

We find the reference temperatures to be T*00K = 631.5 K, and T*400K =

1031.5 K. This gives 5600K/$1,400K « 0.66, which is in good agreement with the measured value « 0.64.

Problem 10.4

The skin friction т of the boundary layer and the skin-friction coefficient cf have the same the reference-temperature proportionality. For turbulent boundary layers it reads

-0.67

cf, turb ^

With that we obtain

Cf, turb, ZOOK cf, turb, 1,600K T, 600K

The free-stream static temperature is TA = 242.22 K. We find the recovery temperature to be Tr = 690.66 K (Pr = 0.74). Because boundary-layer edge data are not available, Te is chosen to be TTO.

With that we find T5*00K = 469.77 K, and T* 600K = 1,019.77 K. This gives cf, turb,500K/cf, turb, 1,600K « 1.68, which is in fair agreement with the measured ratio « 1.66 to 1.4.

A check with Te = 2 T^ yields « 1.6, which shows a relative insensitivity. The result shows that the thermal surface effect on the skin-friction can be explained with the help of the reference-temperature concept. On the other hand the effect can be estimated with that concept, which can be helpful in design work.

Reference

1. Hirschel, E. H., Weiland, C.: Selected Aerothermodynamic Design Problems of Hypersonic Flight Vehicles. Progress in Astronautics and Aeronautics, AIAA, Reston, vol. 229. Springer, Heidelberg (2009)