Special Rotations

Let us build up our confidence by constructing the general rotation tensor from special rotations. Beginning with planar rotations, we extend them to the third dimension and eventually obtain a general formulation that presents the rotation tensor in terms of its rotation axis and angle.

4.1.2.1 Planar rotations. In Fig. 4.31 have plotted two unit vectors b’, and c’, embedded in the plane subtended by the Iа, 2a axes of the coordinate system ]A. Unit vector c’ is obtained by rotating unit vector b’ through the angle ф. We determine the elements of the rotation tensor in the ]A coordinate system. From Eq. (4.1) we deduct, considering the two vectors as base vectors,

[c’]A = [R]A[b’]A (4.8)

To determine [??]A, we calculate first the components of the two vectors from elementary trigonometric relationships:

~СГ	A	"cos(e + ф)		”cos e cos ф — sin e sin ф
C2	=	sin(e – I – ф)	=	sin є cos ф + cos є sin ф
_C3.		0		0

3A

Fig. 4.3 Planar rotation.

and

pi]	A	~cos e~
b’2	=	sine
kJ		0

Substituting both relationships into Eq. (4.8) yields

COS Є COS ф — sin є sin iff		r 11 Г2 rn		cos є
sin Є COS + COS Є sin l/r		Г21 Г22 Г22		sine
0		гзі r32 m		0

Our task is to establish the elements of the rotation matrix ry. By inspection we deduce the first two columns:

To determine the third column, we have to introduce the third dimension.

4.1.2.2

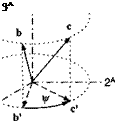Nonplanar rotation. We expand Fig. 4.3 to the third dimension and reinterpret b’ and c’ as the projections of the two vectors b and c of equal height (see Fig. 4.4). To determine the elements of the rotation tensor in the ]’4 coordinate

system, we first recognize that the Iа, 2a coordinate axes of the two vectors [c]A and yb] A are the same as those of the planar rotation example just shown. Second, to determine the remaining last column we apply the fact that the third component of [c]A and [bA remains unchanged. Thus we supplement Eq. (4.9) and receive the three-dimensional rotation tensor

cos ф —sin ф 0 sin ф cos ф 0

0 0 1

Clearly evident is the similarity with the coordinate transformation matrix, but note that the negative sign of the sine function is two rows above the 1 entry and not right above it, as it is the case with coordinate transformations. Be careful however, this derivation is only valid if the rotation is about the third direction. The generalization occurs in the next section.