Symbols and Acronyms
Only the important symbols are listed. If a symbol appears only locally or infrequent, it is not included. In general the page number is indicated, where a symbol appears first or is defined. Dimensions are given in terms of the SI basic units: length [L], time [t], mass [M], temperature [T], and amount of substance [mole], Appendix B. The dimensions are written as ‘a/bc’ instead of ‘a/(bc)’ or ‘a b-1 c-1’. For actual dimensions and their conversions see Appendix B.2.
C.1 Latin Letters
A amplitude, p. 287
A surface, [L2]
a speed of sound, p. 153, [L/t]
C Chapman-Rubesin factor, p. 363, [-]
CD drag coefficient, p. 197, [-]
CL lift coefficient, p. 197, [-]
CR resultant (total) force coefficient, p. 198, [-]
c molar density, p. 29, [mole/L3]
c phase velocity, p. 287, [L/t]
Ci molar concentration of species i, p. 29, [mole/L3]
cp pressure coefficient, p. 155, [-]
cp (mass) specific heat at constant pressure, p. 116, [L2/t2T]
cv (mass) specific heat at constant volume, p. 116, [L2/t2T]
D diameter, [L]
D drag, [ML/t2]
DAM 1 first Damkohler number, p. 120, [-]
DAM2 second Damkohler number, p. 120, [-]
Dab mass diffusivity coefficient of a binary system, p. 86, [L2/t]
D’A thermo-diffusion coefficient of species A, p. 103, [M/Lt]
E Eckert number, p. 99, [-]
e internal (mass-specific) energy, p. 96, [L2/t2]
f degree of freedom, p. 115, [-]
f frequency, p. 287, [1/t]
G Gortler parameter, p. 306, [-]
H altitude, p. 2, [L]
H shape factor, p. 247, [-]
h (mass-specific) enthalpy, p. 116, [L2/t2]
ht total enthalpy, p. 38, [L2/t2]
h* reference enthalpy, p. 234, [L2/t2]
j diffusion mass-flux vector of species i, p. 103, [M/L2t]
K hypersonic similarity parameter, p. 209, [-]
K acceleration parameter, p. 306, [-]
Kc equilibrium constant, p. 123, [(L3/mole)v ]
Kn Knudsen number, p. 31, [-]
k thermal conductivity, p. 84, [ML/t3T]
k roughness height, surface parameter, p. 308, [L]
k turbulent energy, p. 313, [L2/t2]
kfr forward reaction rate, p. 123, [L3/molev -1 t]
kbr backward reaction rate, p. 123, [L3/molev -1 t]
kWia catalytic recombination rate, p. 133, [L/t]
L characteristic length, [L]
L lift, [ML/t2]
Le Lewis number, p. 99, [-]
M Mach number, p. 92, [-]
M molecular weight, p. 29, [M/mole]
M moment, [ML2/t2]
MN Mach number normal (locally) to the shock wave, p. 163, [-]
Mi molecular weight of species i, p. 29, [M/mole]
Mо flight Mach number, [-]
M* critical Mach number, p. 154, [-]
Pe Peclet number, p. 98, [-]
Pr Prandtl number, p. 98, [-]
p pressure, p. 29, [M/Lt2]
pe pressure at the boundary-layer edge, p. 199, [M/Lt2]
pi partial pressure of species i, p. 29, [M/Lt2]
q dynamic pressure, p. 154, [M/Lt2]
qо free-stream dynamic pressure, [M/Lt2]
q heat flux, p. 82, [M/t3]
qgw heat flux in the gas at the wall, p. 38, [M/t3]
qw heat flux into the wall, p. 38, [M/t3]
qrad thermal radiation heat flux, p. 44, [M/t3]
q’ disturbance amplitude, p. 287
R gas constant, p. 29, [L2/t2T]
R radius, [L]
R0 universal gas constant, p. 29, [ML2/t2moleT]
Re Reynolds number, p. 92, [-]
Reu unit Reynolds number, p. 26, [1/L]
Red contamination Reynolds number, p. 300, [-]
r recovery factor, p. 39, [-]
|
|||
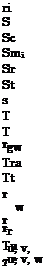 |
|||
|
|
||
|
|||
|
|||
|
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
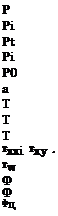 effective ratio of specific heats, p. 178, [-] recombination coefficient of atomic species, p. 132, [-] characteristic boundary-layer thickness, p. 44, [L] shock stand-off distance, p. 176, [L] flow (ordinary) boundary-layer thickness, p. 93, [L] ramp angle, p. 163, [°]
effective ratio of specific heats, p. 178, [-] recombination coefficient of atomic species, p. 132, [-] characteristic boundary-layer thickness, p. 44, [L] shock stand-off distance, p. 176, [L] flow (ordinary) boundary-layer thickness, p. 93, [L] ramp angle, p. 163, [°]
shock stand-off distance (6 = A0), p. 177, [L]
flow (ordinary) boundary-layer thickness (6flow = 6), p. 93, [L]
mass-concentration boundary-layer thickness, p. 104, [L]
thermal boundary-layer thickness, p. 100, [L]
turbulent scaling thickness, p. 243, [L]
viscous sub-layer thickness, p. 242, [L]
boundary-layer displacement thickness (61 = 6і), p. 245, [L]
boundary-layer momentum thickness (62 = в), p. 245, [L]
emissivity coefficient, p. 44, [-]
density ratio, p. 176, [-]
fictitious emissivity coefficient, p. 54, [-]
characteristic dissociation temperature, p. 123, [T]
characteristic rotational temperature, p. 119, [T]
characteristic vibrational temperature, p. 121, [T]
flow angle, p. 78, [°]
shock angle, p. 163, [°]
sonic shock angle, p. 166, [°]
bulk viscosity, p. 90, [M/Lt]
mean free path, p. 31, [L]
wave length, p. 287, [L]
viscosity, p. 83, [M/Lt]
Mach angle, p. 169, [°] kinematic viscosity, p. 227, [L2/t]
Prandtl-Meyer angle, p. 189, [°], [rad]
stoichiometric coefficients, p. 122, [-]
density, p. 29, [M/L3]
partial density of species i, p. 29, [M/L3]
total density, p. 153, [M/L3]
fractional density of species i, p. 30, [M/L3]
surface suction or blowing density, p. 245, [M/L3]
reflection coefficient, p. 94, [-]
relaxation time, p. 121, [t]
thickness ratio, p. 209, [t]
viscous stress tensor, p. 90, [M/t2L]
components of the viscous stress tensor, p. 221, [M/t2L]
skin friction, wall shear stress, p. 256, [M/t2L]
angle, p. 355, [°]
transported entity, p. 79
term in Wilke’s mixing formula, p. 88
p characteristic manifold, p. 227
p sweep angle of leading edge or cylinder, p. 202, [°]
X cross-flow Reynolds number, p. 301, [-]
X, X viscous interaction parameter, p. 364, [-]
Ф’ disturbance stream function, p. 288, [1/t]
ф angle, p. 201, [°]
Q vorticity content vector, p. 218, [L/t]
Qk dimensionless thermal conductivity collision integral, p. 85, [-]
dimensionless viscosity collision integral, p. 83, [-] ш circular frequency, p. 287, [1/t]
ші mass fraction of species i, p. 29, [-]
шк exponent in the power-law equation of thermal
conductivity (шк, шк1, шк2), p. 85, [-] шц exponent in the power-law equation of
viscosity (шм, шмі, шМ2), p. 83, [-]
C.3 Indices
C.3.1 Upper Indices
![]()
![]() i = 1, 2, 3, general coordinates and contravariant velocity components
i = 1, 2, 3, general coordinates and contravariant velocity components
physical velocity component
thermo-diffusion
unit
ionized
dimensionless sub-layer entity reference-temperature/enthalpy value
|
C.3.2 |
Lower Indices |
|
A, B |
species of binary gas |
|
br |
backward reaction |
|
c |
compressible |
|
corr |
corrected |
|
cr |
critical |
|
D |
drag |
|
e |
boundary-layer edge, external (flow) |
|
elec |
electronic |
|
eff |
effective |
|
equil |
equilibrium |
|
exp |
experiment |
|
fp |
flat surface portion |
|
fr |
forward reaction |
|
gw |
gas at the wall |
|
Han |
Hansen |
|
i |
imaginary part |
|
i, j |
species |
|
ic |
incompressible |
|
k |
thermal conductivity |
|
L |
lift |
|
l |
leeward side |
|
lam |
laminar |
|
M |
mass concentration |
|
molec |
molecule |
|
ne |
non-equilibrium |
|
R |
resultant |
|
r |
real part |
|
r |
reaction |
|
r |
recovery |
|
ra |
radiation adiabatic |
|
rad |
radiation |
|
ref |
reference |
|
res |
residence |
|
rot |
rotational |
|
SL |
sea level |
|
Suth |
Sutherland |
|
s |
shock |
|
s |
stagnation point |
|
sc |
turbulent scaling |
|
scy |
swept cylinder |
|
sp |
sphere |
|
T |
thermal |
|
t |
total |
|
tr, l |
transition, lower location |
|
tr, u |
transition, upper location |
|
trans |
translational |
|
turb |
turbulent |
|
vibr |
vibrational |
|
vs |
viscous sub-layer |
|
w |
wall |
|
w |
windward side |
|
R |
viscosity |
|
T |
friction velocity |
|
0 |
reference |
|
1 |
ahead of the shock wave |
|
2 |
behind the shock wave |
infinity
critical
C.4 Other Symbols
O() order of magnitude
‘ non-dimensional and stretched
‘ fluctuation entity
v vector
t tensor
C.5 Acronyms
Indicated is the page where the acronym is used for the first time.
 aeroassisted orbital transfer vehicle, p. 3 ascent and re-entry vehicle, p. 3 blunt delta wing, p. 63 cruise and acceleration vehicle, p. 3 direct numerical solution, p. 296
aeroassisted orbital transfer vehicle, p. 3 ascent and re-entry vehicle, p. 3 blunt delta wing, p. 63 cruise and acceleration vehicle, p. 3 direct numerical solution, p. 296
Future European Space Transportation Investigations
Programme, p. 3
general thermal radiation, p. 54
high alpha inviscid solution (configuration), p. 135
large eddy simulation, p. 313
orbital maneuvering system, p. 52
Reynolds-averaged Navier-Stokes, p. 55
Rankine-Hugoniot-Prandtl-Meyer, p. 19
re-entry vehicle, p. 3
single stage to orbit, p. 3
two stage to orbit, p. 3
thermal protection system, p. 11
[1] A detailed classification of both civil and military hypersonic flight vehicles is given, for instance, in [3].
[2] In [5] non-winged re-entry vehicles (capsules) are considered as a separate vehicle class. Most prominent members of this class are APOLLO and SOYUZ. Capsules flying in the Earth atmosphere at altitudes below approximately 100 km, and with speeds below 8 km/s can be considered as belonging to class 1.
[3] The X-38 was NASA’s demonstrator of the previously planned crew rescue vehicle of the International Space Station.
[4] The experimental vehicles X-43A, [8], and X-51A, [9], were dedicated to the tests of scramjet (supersonic combustion ramjet) and ramjet propulsion systems. In the frame of HIFiRE, [10], HIFiRE-2 and HIFiRE-3 were scramjet flight experiments. Boost-glide vehicles go back to the X-20/Dyna-Soar, which has its roots in German studies during World War II [11]. Such vehicles can be counted as CAV’s, however without a propulsion system.
[5] In Section 1.2 characteristic flow features of two particular flight vehicle classes are discussed in some detail.
[6] We note that, for instance, future RV’s may demand large down and cross range capabilities (see some of the FESTIP study concepts [13] and also [5]). Then aerodynamic lift/drag “small” for RV’s in Table 1.1 actually should read “small to medium”.
A free-stream surface is a vehicle’s surface which is not inclined against the free stream.
[8] Sub-critical means that laminar-transition is not triggered prematurely, and that in turbulent flow neither skin friction nor heat transfer are enhanced by surface irregularities, Chapter 8.
[9] The heat flux is the heat transported through a unit area per unit time.
[10] This is the basic definition. A more general definition would include also the temperature gradients in tangential directions. Such situations can be found at vehicle noses, leading edges, inlet cowl lips, etc., see, e. g., [5, 21]. In nonconvex situations and if shock layer radiation is present, the definition must be generalized further. For our discussions we can stick with the basic definition.
[11] In this book the direction normal to the wall usually is defined as ^-coordinate.
[12] In the space community the aerodynamic data are sometimes called “data of static longitudinal stability”. This stems from the rocket launch technology. During the launch process the rocket flies longitudinally unstable and must be controlled with aerodynamical or engine-related means.
[13] In [13] it is shown, that with a “locally” defined Knudsen number more precise statements can be made.
[14] It is noted already here, that flow-physics models (laminar-turbulent transition, turbulence, turbulent separation), which are required in viscous flow simulations for altitudes below approximately 50 km, partly have large deficits. This holds also for thermo-chemical models in the whole flight regime considered in this book.
[15] This situation is also called radiation equilibrium.
[16] We neglect here also non-convex effects, Sub-Section 3.2.5, and other possible external heat radiation sources.
[17] The reader may note that we usually omit this word in this book, writing simply “radiation cooling”.
recent publication [7, 8].
[19] Regarding this highly complex phenomenon we cite only an early and a more
[20] Note that on a typical Space Shuttle Orbiter trajectory the maximum thermal loads occur around 70 km altitude [2]. Indeed it has been shown exactly that the maximum heat flux qgw in the stagnation point occurs at approximately 73 km altitude [15].
[21] This leads to the dilemma in the design of CAV’s that on the one hand nose and leading edge radii must be small in order to minimize the wave drag, whereas on the other hand they must be large enough to permit an effective surface radiation cooling. This dilemma does not exist for RV’s. They have on purpose large surface radii and fly at large angle of attack for an effective deceleration. The large radii at the same time also very effectively support surface radiation cooling.
[22] Due to the different characteristic angles of attack, Fig. 1.3, the primary (wing) attachment lines at a CAV (small a) lie indeed at the leading edge (see Figs. 7.8 and 7.9 in Section 7.3), but in contrast to that lie at RV’s (large a) on the windward side (see Fig. 3.16 in Section 3.3, and the upper part of Fig. 9.5 in Section 9.1).
[23] In [18] attachment and separation lines as well as the appearance of extremes of the thermal state of the surface across such lines are treated in detail.
[24] Note that the original emissivity coefficient є is a property only of the vehicle surface material.
More results, in particular regarding the flow in the cavity above the split body flap/elevon of the X-38 are discussed in [2].
[26] In three dimensions the coordinate г and the velocity component w are orthogonal to the picture plane.
[27] Often also called diffusive transport.
[28] This transport mechanism is not a central topic of this book, see below.
[29] To be precise, viscous flow due to molecular transport refers to “laminar flow”.
[30] In the literature values for the Prandtl number of air at ambient temperatures are given as low as Pr = 0.72, compared to Pr = 0.7368 in Table 4.4. A gas – kinetic theory value of Pr = 0.74 for T = 273.2 K, compared to an observed value of Pr = 0.73, is quoted in [2].
[31] State surfaces for planet atmospheres are available, too. For CO2/N2 atmospheres (Mars, Venus) see, e. g., [15].
[32] The governing equations need to be applied in conservative formulation in discrete numerical computation methods in order to capture shock-wave and slip surfaces.
[33] Mcrit, iower is the lower critical Mach number, at which first supersonic flow appears at the body surface. For airfoils Mcrit, lower ~ 0.7-0.8. Usually Mcrit, lower is simply called critical Mach number Mcrit.
[34] Mcrit, upper is the upper critical Mach number, at which the flow past the body is fully supersonic except for a subsonic pocket, if the body has a blunt nose. For airfoils Mcrit, upper ~ 1.1-1.2.
[35] Note that in boundary-layer theory the boundary-layer equations are found for Re ^ to, however, only after the “boundary-layer stretching” has been introduced, Sub-Section 7.1.3.
[36] This formulation is also employed in Appendix A, where the whole set of governing equations is collected.
[37] The difference Tgw — Tw is called the temperature jump.
[38] Note that in general in all cases the heat fluxes and temperatures are functions of the location at a vehicle surface.
[39] m / Dab 1
— oc ———- OC :
x ux RexSc
The thickness of the mass-concentration boundary layer 5m is related to the thickness of the flow boundary layer 5 = 5fiow by
[40] For a precise definition see Section 6.8.
[41] We recall the discussion in Section 1.2. We noted there that (high-temperature) real-gas effects are strong on the windward side of RV’s and almost absent on their leeward side due to the large angles of attack, at which these vehicles fly. On CAV’s real-gas effects are small to moderate, depending on the flight speed, but are present, to a different degree, on both the windward and the leeward side due to the low angles of attack.
(C Springer International Publishing Switzerland 2015 E. H. Hirschel, Basics of Aerothermodynamics,
DOI: 10.1007/978-3-319-14373-6 _5
[42] That y is not constant in general is due to the vibrational excitation, see below. The gas is calorically not perfect.
[43] The characteristic temperatures GrotN2, &rotO2, and GrotNO are listed in Appendix B.1.
[44] See Table 4.4.
[45] This is the case of air at low temperatures (T 7 400 K, Sub-Section 4.2.3).
[46] This case can be seen in the frame of the “effective ratio of specific heats” approach [6]. Ysff ~ 1.4 can be used to estimate the influence of high-temperature real-gas effects.
[47] The reader should note that translational non-equilibrium is the cause of molecular transport (Chapter 4) of momentum (viscous stress), heat (heat conduction) and mass (mass diffusion), and rotational non-equilibrium that of bulk viscosity, [1].
Note that all boundary-layer thicknesses are effectively finite at a stagnation point, and in particular along attachment lines, Sub-Section 7.2.1 and [13].
[49] Such a temperature distribution supports the tendency of surface catalytic N2 recombination at the front part of the windward side of the vehicle, whereas O2 recombination occurs only at the colder middle and aft part.
[50] Close to the surface the mass-diffusion velocity is the characteristic velocity vref, Section 5.4. This means a large residence time and hence DAM 1 ^ to. Catalytic wall behavior, however, is amplifying gradients, and in turn also near-wall nonequilibrium transport phenomena.
The heterogeneous reaction can be formulated in analogy to the homogeneous reaction, eq. (5.30), which we do not elaborate further here.
[52] For a recent explanation of the pitching-moment anomaly see [6]. There it is shown that Mach-number independence in the presence of high-temperature real – gas effects appears only to be given, if the (inviscid) wall Mach number is lower than about Mw ~ 2.2.
[53] If the flow behind the shock wave is a subsonic flow, the shock wave is called strong shock wave. If the flow is supersonic, the shock wave is called weak shock wave.
[54] At hypersonic speeds sharp-nosed cones would suffer untenable large thermal loads, so that cases b) and c) are hypothetical at such speeds.
[55] This is important also with regard to the proper choice of reference data in similarity parameters, Section 4.4. Over the CAV the boundary-layer edge Mach and unit Reynolds numbers for instance have approximately the order of magnitude of the free-stream values, Section 1.2. At the RV in particular the boundary-layer edge Mach number Me is much lower: at an angle of attack of a ~ 40° at flight Mach numbers 25 T MT 10 we have a large portion of subsonic flow, and then at most Me ~ 3.
[56] Such a strong-interaction situation is treated in some detail in Sub-Section 9.2.1, third example.
[57] This is to be distinguished from stream-tube flow, where in a tube with varying cross-section uniform distributions of the flow properties are assumed, see, e. g.,
[58] The general formulation in terms of the enthalpy h is h + )u2 = ht, where ht is the total enthalpy of the flow, see also Section 3.1.
[59] We use in this chapter for the convenience of the reader the notation from [11]. There a broad collection of important and useful relations and data concerning perfect-gas compressible air flow is given.
[60] The location of the critical speed of sound is within the viscous shock layer, Fig. 5.4 a). If we consider the shock wave as a discontinuity, a* is a fictitious entity, which is hidden in the discontinuity.
[61] K. Oswatitsch defines hypersonic flow past a body as flow with a free-stream Mach number M^ to. We come back to this in Section 6.8.
This holds for plane flow. At a cone, Fig. 6.14 b), the situation is different.
[63] At a general three-dimensional shock surface, locally the angle between the shock-surface normal and the free-stream direction is 90° – 0. We then define two tangential velocity components at the shock surface.
The effective body shape is the shape, which the free-stream flow “sees”, i. e., the configuration of the flight vehicle at angle of attack, yaw, etc.
[65] Shock waves belong to the same family, if their shock angles в have the same sign. This sign is the same as that of the angles (Mach angles p) of the respective Mach lines (characteristics) of the flow in which they are imbedded [4, 6]. The shock waves belong to opposite families, if their shock angles have opposite signs.
[66] Actually the body contour and these phenomena together with the free-stream properties determine the shape of the bow-shock surface.
[67] We have introduced both the normal and the oblique shock as phenomenological models. They are not curved, and hence we find constant entropy behind them from streamline to streamline.
[68] For the influence of the Mangler effect and the surface temperature on the boundary-layer thickness see Sub-Section 7.2.1.
[69] For the problem of defining this thickness see also Sub-Section 7.2.1.
[70] Actually it is the displacement thickness of the boundary layer which is a streamline [7]. In three dimensions it is a stream surface.
[71] Indeed, it is only in first-order boundary-layer theory, where the boundary layer is assumed to be infinitely thin, that the inviscid streamline at the body surface is considered as the edge streamline of the boundary layer.
[72] We will see below, that the boundary layer first of all must be thick enough that the effect can happen.
[73] We assume isoenergetic inviscid flow, where the total enthalpy is constant in the whole flow field. Hence for a given free-stream Mach number the (static) temperature behind the shock wave is the smaller the smaller the shock angle в is, eq. (6.85).
[74] This very accentuated step behavior is due to the properties of the employed approximate method. Note that the strong interaction phenomena present at the ramp junctions—Sub-Section 9.2.1—are not captured by that method. The result hence reflects on each ramp the so called asymptotic behavior of the flow [2].
This side in Newton flow is the “hypersonic shadow” side of the flat plate.
[76] For the circular cylinder к = /2 is given in [42] as a more adequate value.
[77] The normal-shock values are included with в = 90°.
[78] We call it Oswatitsch’s independence principle because he was the one who has given the observations and hence the Mach-number independence principle a sound mathematical foundation.
[79] That Mach number independence for the sphere is reached at lower Mach numbers than those for the cone-cylinder is due to the fact that the bow-shock surface of the former has a larger portion with large shock angle в.
This is permitted, because a constant term is subtracted from the argument of grad s in eq. (6.176).
This result is analogous to that which we obtain for incompressible flow by means of the Laplace equation.
[82] It practice it depends on the design margins where M^ can be placed.
[83] Tsien neglects in this work the occurrence of shock waves and hence obtains results of restricted validity [44].
[84] We remember that three kinds of boundary layers can be present simultaneously: flow, thermal, and mass-concentration boundary layers, Section 4.3.
[85] We remember that the boundary-layer edge is not a streamline, Sub-Section 6.4.2, or here, a stream surface, nearly parallel to the body surface. Only in first-order boundary-layer theory, where the boundary layer is assumed to be infinitely thin, can the inviscid flow at the body surface considered to be the edge flow of the boundary layer. Here it would be the local projections of the loci, where the streamlines cross the boundary-layer edge.
[86] The reader will have noted that we have figures in the text with other notations. We always point this out, because no general nomenclature has been adopted so far in the literature. General surface-oriented “locally monoclinic” coordinates, which make use of the notation of shell theory, denote the tangential coordinates with x1 and x2, whereas the coordinate normal to the body surface is x3 [1]. Accordingly we have the physical velocity components v*1, v*2 and v*3.
[87] The Chapman-Rubesin criterion in any form is of importance only for boundary – layer methods, viscous shock-layer methods, and for thin-layer formulations of the Navier-Stokes/RANS equations. In the full Navier-Stokes or RANS equations the terms in question are present anyway.
[88] Note that locally the boundary-layer edge Mach number Me is relevant, see Section 4.4. This means that the above equations can be employed—if necessary in second-order formulation—on both CAV’s and RV’s, the latter having at the large angles of attack only small boundary-layer edge Mach numbers, Section 1.2.
[89] There are other higher-order effects, which we do not mention here, see, e. g., [11].
The surface boundary conditions for general hypersonic flow have been discussed in detail in Section 4.3.
[91] It is the classical interpretation that an adverse pressure gradient leads to a profile u(y) with a point of inflection, but zero and favorable pressure gradient not. With our generalization we see that also other factors can lead to a point of inflection of the profile u(y).
Regarding the exponent ш we have to keep in mind the temperature interval of the considered problem.
11 Since the unstable behavior was initially observed in explicit solution schemes, it was attributed to a singularity at the location in the flow where M(y) = 1. In
[94] it was shown that the singularity is only an apparent one, and then in [18] that the system of equations is of elliptic/parabolic type in the subsonic part of the flow, if the pressure-gradient term in eq. (7.75) is not omitted.
We call the sum of the skin-friction drag and the form drag in summary “viscous drag” [1].
[96] This Reynolds number can also be formulated as Ree, x in terms of the boundary – layer edge flow properties, or fully generalized as Reref, x, if a suitable reference state can be established.
[97] In the case that the inviscid flow is not known, e. g., in Navier-Stokes/RANS
solutions, but also in experiments, the boundary-layer edge can be defined by vanishing boundary-layer vorticity A e [23]. However, if shock/boundary-
layer interaction has to be taken into account, such a criterion needs to be refined.
[98] The 4-th-power law approach is detested by some authors. Of course there are other more accurate relations. However, if qualitative considerations are to be made, it is, together with the reference-temperature extension, the best approach. This holds also for quick estimations of boundary-layer properties. If a high accuracy is needed, discrete numerical methods together with elaborate turbulence models, Section 8.5, anyway are to be employed. Modern hybrid RANS-LES approaches even permit to describe massively separated flow. The biggest challenge—if a flight vehicle is transition sensitive—still is the accurate and reliable prediction of the location and the properties of the laminar-turbulent transition zone in a typical hypersonic flow environment, Section 8.1.
[99] In the following we denote thicknesses of compressible boundary layers with V and those of incompressible ones with ‘ic Regarding the choice of the exponent ш in the viscosity law, the temperatures must lie, at least approximately, in the same temperature interval.
[100] In the literature often 4* and в are used instead of and S2.
[101] This is in contrast to two-dimensional boundary layers, where 41 is always positive, except for extremely cold wall cases [1].
[102] Navier-Stokes/RANS solutions do not explicitly exhibit these properties of attached and separating viscous flow. They can be found by a post-processing of the computed results with eq. (7.107) to (7.109).
[103] The name momentum thickness is used throughout in literature [21]. Actually it is a measure of the loss of momentum in the boundary layer relative to that of the external inviscid flow, and hence should more aptly be called momentum-loss thickness.
[104] Also here it holds that for flat plates at zero angle of attack, and hence also at CAV’s at small angle of attack, except for the blunt nose region, we can choose ‘ref ’ = W, whereas at RV’s the conditions at the outer edge of the boundary layer are the reference conditions: ‘ref ” = ‘e’.
The larger T*/Tref, the larger are the boundary-layer thicknesses, except for the momentum thicknesses S2,lam and S2,turb. For a given Mref and a given Tref an increasing wall temperature Tw leads to an increase of the laminar boundary-layer thicknesses Slam and S1ilam (ж (T*/Tref)0 825), which is stronger than the increase of the turbulent boundary-layer thicknesses 5turb and S1iturb (ж (T*/Tref )0 33). Strongest is the increase of the thickness of the viscous sub-layer Svs, ж (T*/Tref )1’485, and that of the turbulent scaling thickness, ж (T*/Tref)132. Concerning the momentum thicknesses, that of the turbulent boundary layer decreases stronger with increasing wall temperature than that of the laminar boundary layer.
These are the basic dependencies of flat-plate boundary-layer thicknesses on flow parameters and wall temperature. On actual configurations other dependencies exist, which are mentioned in the following. In general no explicit
We take к here as a representative permissible surface property, like surface roughness, waviness, etc., see Section 1.3. It influences boundary-layer properties, if it is not sub-critical, Section 8.1. A roughness к is critical, if its height is larger than a characteristic boundary-layer thickness, for instance the displacement thickness Si (Sub-Section 8.3). It must be remembered, that boundary layers are thin at the front part of flight vehicles, and become thicker in the stream-wise direction. The influence of surface roughness and the like on laminar-turbulent transition, turbulent wall-shear stress and the thermal state of the surface is known, at least empirically [21, 24]. Its influence on S, however, which probably exists, at least in turbulent boundary layers, is not known.
[105] Although it is actually only one boundary layer, which develops over the vehicle’s surface, usually the boundary layers on the lower and the upper side of the configuration are distinguished.
[106] We remember that for flat plates at zero angle of attack, and hence also at CAV’s at small angle of attack, except for the blunt nose region, we can choose ‘ref ’ = W, whereas at RV’s we must choose the conditions at the outer edge of the boundary layer: ‘ref ’ = ‘e’.
The larger T*/Tref, the smaller is the wall shear stress. For a given Mref and a given Tref an increase of the wall temperature Tw leads to a decrease of the wall shear stress of a turbulent boundary-layer (tWi turb ж (T*/Tref )-0 67), which is stronger than the decrease of the wall shear stress of a laminar boundary-layer (tWi lam ж (T*/Tref )-0175). A drag-sensitive hypersonic of CAV with predominantly turbulent boundary layer therefore should be flown with a surface as hot as possible. (But see the discussion in Section 10.7.)
These are the basic dependencies of the wall shear stress of flat-plate boundary-layers on the flow parameters and the wall temperature. On actual configurations dependencies exist, which are similar to the dependencies of the boundary-layer thickness 6 mentioned in Sub-Section 7.2.1. In general it holds that a larger boundary-layer thickness leads to a smaller wall shear stress. Important is to note, that a super-critical roughness of the surface will increase the wall shear stress of turbulent boundary layers [21, 24]. The laminar boundary layer in such a case might be forced to become turbulent (unintentional turbulence tripping). A drag-sensitive CAV must have a surface with sub-critical roughness etc. everywhere.











