Vortex Methods

The free-vortex method (FVM) is a technique related to the VTM (see Sec­tion 10.7.6). In many practical problems involving the rotor wake it can be justified that the structures produced by viscous effects (such as the internal structure of the vortices making up the rotor wake) have very much smaller length scales compared to the structures produced by purely potential flow (such as the global deformation of the wake). This allows concentrated regions of vorticity to be represented as singularities within the flow, in which case Eq. 14.15 reduces to the inviscid equation

Helmholtz’s second law states that the vortex lines move as material lines – see Saffman

(1992) . This can be shown as follows. Consider a material segment 5s somewhere in the flow. The equation of motion for this vortex segment in Lagrangian form is given by

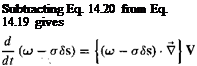(14.20)

(14.21) for some time-independent a. If at some time t = to the material line happens to coincide with the vortex line, then (u>o — o-5so) = 0. If the velocity field is continuous, then it follows that Eq. 14.21 has only one unique solution, namely (со — a5s) = 0. In other words, the local vorticity translates and rotates for all time as a vector that remains aligned with the material segment 5s.

In the vortex method, the dynamics of material lines in the fluid can be used to represent the dynamics of a set of discrete vortex segments, which can be defined in 3-D space by poi nts or Lagrangian fluid markers – see Fig. 10.26 for instance. The motion of the material lines (and fluid markers) reduces to a simple advection equation of the form

— =V, r(r=0) = r0,

dt where г is the position vector of a marker, Tq is the initial position vector of the marker, and V(r) is the local fluid velocity at that marker. The solution of Eq. 14.22 is complicated significantly, however, by the highly nonlinear nature of the velocity field, V.

There are many different approaches to the solution of Eq. 14.22 for helicopter rotor wake problems, all of which involve the repeated evaluation of the Biot-Savart law to calculate the velocity field У in terms of the vorticity in the flow. Both time marching (time integration) and relaxation (iterative) methods can be employed – see Leishman, Bhagwat, & Bagai (2002) and Wachspress et al. (2003). An example of a wake calculation using the vortex method is shown in Fig. 14.3. The numerical technique used to obtain the results illustrated here was based on a refinement of the basic FVM using lines of constant circulation strength (see also Fig. 10.26). The vortex method has the advantage of being free of artificial diffusion; the vortex filaments are essentially self-adapting and do not dissipate. This means that the wake well downstream of the rotor remains very well defined compared to most Eulerian grid-based solutions, although care must be taken to avoid deterioration of accuracy if the marker points used to define the wake structure begin to drift apart downstream of the rotor.