Vorticity Transport Equations
The use of vorticity transport models has seen some recent success in modeling the vortical flow structure of helicopter rotor wakes. This approach is intermediate between the Navier-Stokes and Euler based CFD techniques described in the previous sections and the ffee-vortex method (FVM) discussed in detail in Section 10.7.6. As previously mentioned, discretized approaches to solving the governing equations of the flow can suffer excessively from numerical dissipation of vorticity, for instance, in the rotor wake. This renders these approaches effectively useless for calculations where flight conditions force the vortical structures in the rotor wake to persist near the rotor for very long times, such as for flight in ground effect or in descending flight. Flight approaching the vortex ring state proves to be a particularly good example – see Section 14.10.7. If the flow can be assumed to be incompressible (generally a reasonable assumption in the rotor wake), vorticity transport methods can be used to overcome the problem of diffusion of vorticity. This is done by solving the governing equations for the flow not in the conservative variable form described previously but directly in terms of the variables of vorticity ш and velocity V.
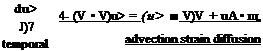 |
|
If the flow is assumed to be incompressible, then, in an Eulerian frame of reference, the Navier-Stokes equations can be rewritten as
where the vorticity w = V x V. The first term in this equation is the temporal evolution of vorticity, the second is an advection term, the third is a strain or stretching term, and the fourth represents viscous diffusion effects. Notice that the stretching term can only exist in a 3-D flow. Alternatively, in Lagrangian form this equation can be written as
Deo
—— = (ш ■ V)V + yA – u>. (14.15)
strain diffusion
Equation 14.15 defines the change of vorticity of a fluid element moving with the flow. This is a Lagrangian representation and is a useful frame of reference to adopt for the vortex methods outlined in the following section (and detailed in Section 10.7.6), whereas Eq. 14.14 defines the change of vorticity at a specified point in the flow, which is an Eulerian representation and is a more useful description for the grid-based CFD method described below.
If the vorticity field is known (or initially assumed), then the velocity field can be calculated using the Biot-Savart relationship
V2V = – Vxw. (14.16)
In practical applications it can be easier, however, to solve this equation in its more familiar integral form as
V(x) = – f – p—~ x ш(у) dy, (14.17)
477- J |X – y|3
The use of this equation is explained in more detail in Section 10.7.1.
The vorticity transport model (VTM) developed by Brown (2000) and Line & Brown
(2004) employs a direct computational solution of Eqs. 14.14 and 14.16 to calculate the evolution of the rotor wake. The development of the rotor wake can be modeled using the vorticity transport equation if the essentially viscous process of vorticity creation as a byproduct of the generation of aerodynamic loads on the rotor blades, fuselage, and so on, is modeled by appending a source term S to Eq. 14.14 to yield
+ (V • V)uj — (u> • V)V = vA • o/+ S. (14.18)
at
If a suitable model for the generation of aerodynamic loads on the system can be defined in terms of the flow velocity V, then the source term allows the effects of the strength and geometry of the vorticity distribution in the rotor wake to feed back into the aerodynamic loading and blade response. This can be done, for instance, by writing S in terms of the shed and trailed vorticity from the blades using a lifting-line or lifting-surface approach – see Section 14.9.
After casting the equations on a structured Eulerian computational grid surrounding the rotor, the velocity field is obtained either by solving Eq. 14.16 for instance by cyclic reduction [see Schumann & Sweet (1976)] or by evaluating Eq. 14.17 using a fast multipole summation technique [see Line & Brown (2004)]. The key feature of the method is that the convection
|
Figure 14.2 Longitudinal plane through the wake of a rotor in low speed forward flight as calculated using the VTM approach. Notice the upwash at the front of the rotor disk and the development of a vortex pairing instability in the wake downstream of the rotor, a physical feature only observed if the vorticity can be preserved for many rotor revolutions. Source: Image courtesy of Andrew Line & Imperial College, University of London. |
of the vorticity through the computational domain is computed using a total variation diminishing (TVD) algorithm [for instance, Toro’s Weighted Average Flux method – see Toro (1989)] that acts directly on the vorticity field, rather than on the density, pressure, and velocity as in more conventional CFD approaches. Very tight control is, therefore, maintained in the VTM over the rate of dissipation of vorticity in the wake and so vortical structures retain their strength and geometry, and are sharply resolved – even though their interactions with the rotor may continue over many rotor revolutions.
An example of a VTM calculation of the wake of a rotor operating in level forward flight at low airspeed is shown in Fig. 14.2. Notice how three levels of grid refinement have been used to resolve the flow very sharply near the rotor while reducing the computational expense in capturing the wake far from the rotor where it has a smaller influence on the rotor behavior. This type of model is very good at representing blade-wake interactions, as well as the wake-wake interactions that, as shown in Fig. 14.2, drive the development of very complicated flow patterns far downstream of the rotor. Although the VTM provides a very complete model for the evolution of the stmcture of the rotor wake, like all grid – based CFD approaches it is computationally expensive for routine use in parametric design applications. It does, however, offer one approach for the practical investigation of a wide range of helicopter rotor wake related issues until such time that Navier-Stokes solutions become more practically feasible.












