Definition of Moment-of-lnertia Tensor

A material body is a three-dimensional differentiable manifold of particles pos­sessing a scalar measure called mass distribution. Integrating the mass distribution over the volume of the body results in a scalar called mass (see Sec. 2.1.1). If the integration includes the distance of the particles relative to a reference point, then we obtain the first-order tensor that defines the location of the c. m. wrt the refer­ence point. If the distance is squared, the integration yields a second-order tensor called the inertia tensor.

Definition: The inertia tensor of body В referred to an arbitrary point R is calculated from the sum over all its mass particles m, and their displacement vector siR according to the following definition:

(6.1)

where SiR is the skew-symmetric form of the displacement vector slR.

The notation IHR reflects the reference point as subscript R, the body frame as superscript В and summation over all particles. The expression siRsiRE— siRsiR — SiRSiR is a tensor identity, which you can prove by substituting components and multiplying out the matrices.

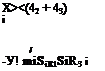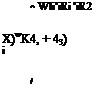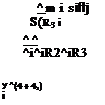For the body coordinates ]B with [.v,«]л = [siRl siR2 siR}], the MOI tensor has the component form

The MOI tensor expressed in any allowable coordinate system is a real symmetric matrix and has therefore only six independent elements. Its diagonal elements are called axial moments of inertia and the off-diagonal elements products of inertia. They have the units meters squared times kilograms. Some examples should give you more insight.

Example 6.1 Axial Moment of Inertia

The axial MOI /„ of the MOI tensor IR about a unit vector n through point R is the scalar

/„ = itIBn (6.3)

It has the same units of meters squared times kilograms as the elements of the MOI tensor. If we select the third-body base vector as axis and express it in body coordinates [nB = [0 0 1], then

	hi hi hi		‘O’
О о If	hi hi hi		0
	hi hi hi		_1_

The 3,3 element was picked out by n, justifying the name axial moment of inertia.

Example 6.2 Lamina

A lamina is a thin body with constant thickness (see Fig. 6.1). If the lamina extends into the first and second direction, then the polar moment of inertia about

3B

the third axis is

I33 = hi + hi (6.4)

For a proof we set sm3 ~ 0 in Eq. (6.2), then

h 1 = m‘sk ’ 7зз = mi (4, + 42)

І І І

Substituting the first two relationships into the third completes the proof.