Derivation of aerodynamic derivatives

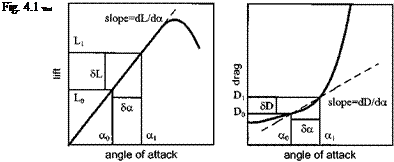
So far, the discussion has been restricted to force changes caused by modifications to the angle of attack. Also small changes (smallperturbations) and linear rates of change have been assumed. A completely general approach would be to include other variables and to allow for non-linear changes. A series of Taylor expansions provide us with a convenient method of expressing these more complex relationships. Therefore, with reference to the body axes [4.2]:

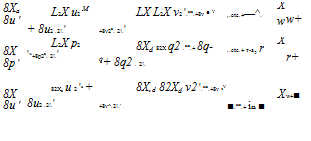
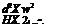
. —… etc.

LX 82X P2 LX 82X f LX L2X r2

+X •p +~LpX. гт^+І^ •q+~dX. i…etc.+17 •r +17. 27^

+ higher-order terms

where

Xa = aerodynamic X-force

Xae = equilibrium X-force generated when the aircraft is in trim u = change in longitudinal speed from trim v = change in lateral speed from trim

w = change in vertical speed from trim p = change in roll rate from trim q = change in pitch rate from trim r = change in yaw rate from trim

u = longitudinal acceleration v = lateral acceleration

w = normal acceleration p = roll acceleration q = pitch acceleration r = yaw acceleration.

-ТГ -r. л л л л л л Xa = Xae + 17 • U +17 • V + 17 • W +1P" •P +17 • q +ИІ ■ Г

If the small perturbation assumption is retained it is again possible to linearize factors in this more complex relationship. Thus if second and subsequent terms in each Taylor series are assumed to be negligible then:

Now applying standard aero-derivative notation:

Which leads to:

Xa — Xae + Xu. u + Xv. v + Xw. w + Xp. p + Xq. q + X. r + Xu. u + Xv-. v

+ Xw. w + Xp. p + Xq. q + X. r

And applying the same analysis to the other forces and moments acting on a helicopter yields the following set of aero-derivatives:

Xu	Xv	Xw	Xp	Xq	Xr	Xu	Xv	Xw	Xp	Xq	X
Yu	Yv	Yw	Yp	Yq	Y	Yu	Yv	Yw	Yp	Yq	Y
Zu	Zv	Zw	Zp	Zq	Zr	Zu	Zv	Zw	Zp	Zq	Zr
Lu	Lv	Lw	Lp	Lq	Lr	Lu	Lv	Lw	Lp	Lq	Lr
Mu	Mv	Mw	Mp	Mq	Mr	Mu	Mv	Mw	Mp	Mq	M
Nu	Nv	Nw	Np	Nq	N	Nu	Nv	Nw	Np	Nq	N

Table 4.1 Force derivatives.

Table 4.2 Moment derivatives.

Using the body axes system it is possible to give a precise meaning to each of the aero-derivatives introduced above, see Tables 4.1 and 4.2.

When the pilot moves a control in the cockpit he will cause changes to the pitch of the appropriate rotor blades. These control inputs will in turn generate off-trim forces and moments in a manner analogous to the effect of gusts. It is possible therefore to identify a set of control derivatives based on the following control deflections from trim, see Table 4.3:

A1 or 01s = lateral cyclic pitch

B1 or 01c = longitudinal cyclic pitch

0c = collective pitch

0TR = tail rotor collective pitch

Forward, side and vertical force due to lateral cyclic pitch Forward, side and vertical force due to longitudinal cyclic pitch Forward, side and vertical force due to collective pitch Forward, side and vertical force due to tail rotor pitch

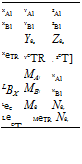
Rolling, pitching and yawing moment due to lateral cyclic pitch Rolling, pitching and yawing moment due to longitudinal cyclic pitch Rolling, pitching and yawing moment due to collective pitch Rolling, pitching and yawing moment due to tail rotor pitch