LIFT FORCES ON STRUCTURES

The drag force produced on fixed buildings or structures is considered in Chapter IV of “Fluid-Dynamic Drag”. The lift force generated on the structure is also an impor­tant design element, especially in the design of roofs and structural overhangs. Also, the lift force produced on smaller objects is important as these can become airborn and cause damage under certain conditions.

Ambient Wind Characteristics.!о determine the wind gen­erated loads on buildings, the worst ambient conditions that would occur in a given time span are used. These would be, for instance, the worst mile of wind over a period of say 50 years and would not necessarily include the winds generated as a result of tornados or hurricanes. In certain instances it is necessary to consider the forces and pressures generated as a result of tornados and hurri­canes where a large loss of lift might be involved.

Fastest Mile Wind. The average speed of one mile of air passing an anemometer is defined as the fastest mile wind. This definition is used as a basis for design so that the effects of gusts that are small with respect to the structure will be eliminated. Charts of the occurrence of the fastest mile-speed are given for the United States at a height of 30 feet above the ground (16,b). In calculating the loads due to the fastest mile wind corrections are made for the exposure, wind profile gradient as a function of terrains and gusts, figure 22. The velocity at any height is deter­mined from the equation

Vz = VG (Z/Za t (11)

where V is the velocity at any height Z and V and Z are standard values adopted (16,a) for various terrains, figure 22, and are given in the table

Terrain	(ft)	l/of
Open Country	900	1/7
Suburban	1200	1/4.5
City	1500	1/3

GRADIENT VELOCITY Figure 22. Wind profile variation with height for city, suburban and open country locations.

The characteristics of hurricanes and tornados are needed for the design of structures; such as atomic power plants, and associated structures.

Hurricanes (16,b). Hurricanes are defined as tropical cyclones with a speed of at least 74 mph. The wind field is a function of the radius of maximum winds, the central pressure difference and forward speed. The strongest winds occur along the rim of the eye near the wall cloud. The wind speed will often reach a speed of 100 ter 135 mph with winds of over 200 mph occurring in severe storms. The damage on structures produced by such high winds where the dynamic pressure can exceed 50 is usu­ally severe.

Tornados. One of nature’s most violent phenomena is the tornado. Although its horizontal extent is small it is char­acterized by a visible funnel, which contains dust and debris extending downward from the base of a cumlo – nimbus cloud of a thunderstorm. The winds and motion of air in a tornado vortex can be divided in four com­ponents; translational, rotational, vertical and radial. At the ground level the translational and rotational com­ponents are most significent. The translational speed of a tornado is anywhere from 0 to 70 mph with the usual speed being 40 to 45 mph. The maximum rotational speeds are believed to be based on wind damage estimates from 200 to 300 mph. With q’s up to 230 psf widespread damage is certain. In the core of the tornado the pressure can be 3 psi below the ambient. With this low pressure and the high winds, large objects can become airborn and cause large amounts of damage when striking stationery structures.

At altitudes above Ze the gradient velocity is assumed to be constant.

The effect of the direction of the exposure and gusts are covered by various standards (16,a, b) and should be used to find the true speed for finding the loads on a given structure.

(16) Lift in buildings and structures:

a) American National Standards Institute, Standard Building Code Requirements, ANSI A58.1-1972.

b) Defense Civil Preparedness Agency, “Multi Protection De­sign” TR-20 (Vol 6) Dec 1973.

c) Ackeret, “Aerodynamics in Structural Engineering” RAE LT 1185 (1965).

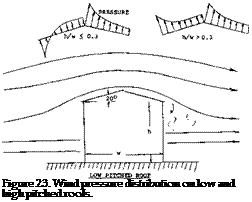
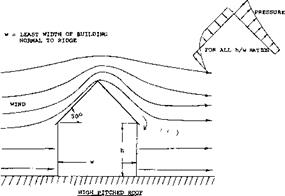Lift in Structure Design. The lift forces generated on the various parts of a building must be determined and con­sidered in their structural design. These forces can be as important as the drag forces discussed in “Fluid-Dynamic Drag” and generally are more poorly understood (16,c). The lift forces on a structure generally effect the roof design as large negatvie pressures in combination with positive pressures, as illustrated on figure 23, produce high loads. Based on the effective pressure as determined based on the fastest mile wind corrected for height, terrain and exposure as discussed previously, the effective dynamic pressure is calculated from the equation:

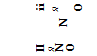where q is the basic wind pressure based on the fastest mile of wind at a height of 30 feet. is the velocity pressure coefficient at height Z from equation (12) and G is a gust factor (16,b). The subscripts F and P correspond to the effective velocity pressure for the full building or a part.

Based on qr or qp above, the standards have been gen­erated (16,a) for establishing the pressure coefficients. These depend on the type of roof. A Cp of —0.7 is typi­cal of gable roofs on the leeward slope. At ridges, eaves and sharp corners the Cp varies from —1.7 to —5.0. In addition to (16,c) estimates of Cp can be estimated from the data given in Chapters II, III and XVII..

Tall Buildings, Towers, Stacks. Structures that are tall where the height exceeds the base by a factor of 5 or greater can be subjected to dynamic effects. For instance, round smoke stacks can have a natural frequency near the vortex shedding frequency as determined using figure 2&4. Similar problems are found with other tall str uctures and should be checked.

[1] Theoretical advancement of aerodynamics: *

a) Prandtl, Necrology, see Journal Aeron Sciences 1953 p 779.

b) Lanchester, “Aerodynamics”, London 1907; and “Aero – netics”, 1908.

c) Prandtl, “Essentials of Fluid Dynamics”, Traro New York 1952.

d) The aerodynamic center of airfoils and/о" wings was established by v. Mises (1917 and 1920) and quoted or re­peated by Munk (1922), Glauert (3,f), Durand (3,i), and Theodorsen (NACA Rpt 383 and 411).

e) Dryden, Karman’s Contributions, Astronautics Aerospace Engg July 1963.

0 Glauert, “Aerofoil and Airscrew Theory”, Cambridge 1926.

g) Schlichting, “Boundary Layer Theory” (1951, 1965), McGraw Hill 1955.

i) Durand, 6 volumes of “Aerodynamic Theory”, 1934/36/43.

[2] Experimental fluid dynamics (wind tunnels):

a) Otto Lilienthal, Rotating Arm, see reference (2,b).

b) Flachsbart, History of Experimental FIJid-Dynamics (from the Greeks to past 1900), Volume IV-2 of Wien-Harms “Handbook Experimentalphysik” (1932).

c) Eiffel, Recherches de ГАіг et TAviation, Paris 1910 and 1914.

d) Ergebnisse AVA Gottingen, Volumes I (1920) II (1923) III (1927) IV (1934).

e) Lewis: “The model test may be considered as an anlogue type of computer”, stated in Transactions SNAME 1954 p 431.

f) Schulz, Design and Use of Tunnels. Luftfahritechnik 1958 p 1 05.

g) Hoerner, Design and Operation of a WaterTunnel. Fieseler Rpts 1939.

[4] Characteristics and description of wind tunnels:

a) Prandtl, Wind-Tuunel Design, in Wien-Harms Handbook Vol IV-2 (1932).

b) Hoemer, Survey of European Tunnels, Z. VDI 1936 p 949.

c) DeFrance, Full-Scale Wind Tunnel, NACA Rpt 459 (1933).

d) Schaefer, Wind Tunnels at Langley Field, NASA 1M X-1130 (1965).

e) Hoerner, Spheres and Turbulence, Lufo (March 1935) p 42; NACA TM 777.

f) Hoerner, TH Brunswick Wind Tunnel, Luftf Forschurg 1937 p 36.

g) Schuh, Tunnel Turbulence and Noise Measured, ARC RM 2905 (1957).

h) Anon, National Wind-Tunnel Summary, NASA and De­fense Department (1961), available from U. S. Department of Commerce.

[5] General and varied information on applied aerodvanmics:

a) Goldstein, “Modern Developments Fluid Dynamics”, Lon­don 1938.

b) Eck, “Technische Stromungslehre”, Springer 1941 aid 1961.

c) rhwaites, “Incompressible Aerodynamics”, Clarendon C <- ford 1960.

[6] Physical properties and characteristics of water:

a) See tor example in Transactions INA (London) 1953 p 35 8.

b) See in chapter I of kT luid-Dynamic Drag”.

c) The salinity in the Dead See is 2 2%. The corresponding density ratio as against fresh water is estimated to be 1.2 6.

[9] Consideration of dynamic stability:

a) Braun, Static Stability, Ringbuch Luftfahrtechnik LB-6 (1940).

b) Jones, Airplane Dynamics, in Volume V of Durand (3,1).

c) Rodgers, Neutral Point, AIAA J. Aircraft 1965 p 33 and 352.

d) Carlson (Wright-Patterson AF Base), Analysis of Stability and Control of Lockheed C-5A Airplane, Astronautics V Aeronautics 1965 p 60.

[10]

(F^, ) is as in equation 42. Note that numerically, W(kp) = m(kg). The “huge” airplane is assumed cruising at an altitude of 10 km, where air density is less than half of that at sea level. The hydrofoil boat is “flying” in (or above) water, where density is a 1000 times that of atmospheric air at an altitude of 2 km.

[12]

[13] Early investigations of wing sections:

a) Lilienthal, “Vogelflug/Fliegekunst”, Berlin 1889.

b) Eiffel, “La Resistance de l’Air et FAviation”; and "Nouvelles Re( herches. . .” Paris 1910, 1919.

c) Munk (k others), Systematic Tests, Tech Berichte der Fliegertruppen Vol I (1917) and Vol II (1918).

[14] Practical information on foil sections and their mechanics can be found in engineering books, such as:

a) Diehl, “Engineering Aerodynamics”. Ronald 1936.

b) Prandtl, “Fiihrer Stromungslehre”, 1942; “Essentials of Fluid Dynamics”, London к New York 1952.

c) Goldstein, “Developments in Fluid Dynamics”, 1936.

d) Schlichting,’Boundary Laver Theory,’ Mc-Graw-Hil

e) Wood. “Aircraft Design”. Author Uni Colorado, 1965.

f) Pope. “Wing and Airfoil Theory”, McGraw Hill

[15] McLarren, “Wright Fiver", Aero Digest July 1953.

[16] Theory and tunnel testing of [oukowsky sections:

a) (oukowsky, Zeitschr Flugtech Motorluft РЖ).

p 281; also in his “Aerodvnamique”, Paris 1916.

b) AfA Gottingen, 36 Foils. Erg III к IV (1927/32).

c) Glauert. Generalі/.(ч’1 Family. .ARC’ RM 911 (1924).

d) ARC, Series 4‘ested. RM 1241 (1929) A 1670(1931,0.

[17] British information on airfoil sections:

a) Pankhurst, NPL Catalogue, ARC C’Paper 81 (1952).

b) Experimental results are found in (36).

c) Nonweiler, Survey, Aircraft Engg 1956 (July).

[18] Riegels, “Aerodvnamische Profile”, Mimchen 1958;

Theorv 8c Experimental Results Over Past 30

[19] Reflexed foil sections for airplane wings:

a) Defore, In V’Densitv Tunnel, NACA TN 388 (1931).

b) Jacobs, “M” Series Foils, NACA Rpt 532 8c 628.

c) 23012 (figure 5) considered to be reflexed?

tl) 2-R-12 Sections in VD Tunnel, NACA TR 460.

e) Moscow, ‘B’ Airfoils, САНІ Rpt 903 (1923).

0 British RAF-34 (figure 3), ARC RM 1771 (1936).

g) For supercritical M’Numbers, NACA T’Rpt 947.

[20] Fage, Lift and Drag = f(A), ARC RM 903 (1923).

[21] For example, a = 4 (as in the 64 Series of NACA airfoil sections) means that at design lift, pressure due to camber remains at its minimum plateau up to x = 0.4 c.

[22] flow pattern and mechanics of vortices:

a) Betz, About Vortex Systems, NACA TM 767.

b) Newman, Trailing Vortex, Aeron Quart 1959 p 149.

[23] Characteristics of elliptical sections:

a) Williams, Elliptical in CAT, ARC RM 1817 (1937).

b) Polhamus, Non-Circular, NASA TR R-46 (1959).

c) Dannenberg, “Airfoil” w’Suction, NACA TN 3498. (1955).

d) Gregory, Thick with Suction, ARC RM 2788 (1953).

[24] Characteristics of sharp-nosed sections:

a) Daley, 6% Thick Sections, NACA TN 3424 (1955).

b) DVL, Double-Arc Sections, see (6) or (34,c).

c) Solomon, Double Wedge, NACA RM A1946G24.

d) Critzos, 0012 to cx 180°NACA TN 3361, 3241.

e) Lift in reversed flow similar to that in (d) for 2212,

Ybk D Lufo 1938 p 1-90 (NACA TM 1011).

f) Lock, Symmetrical Also Reversed, ARC RM 1066 (1926).

g) Polhamus, Drag Due to Lift, NACA TN 3324 (1955).

h) Williams, 4 Circular Arc Foils, ARC RM 2301 (1946).

i) Note that flow does go around leading edge (“no” boundary laver vet), to considerable degree.

[25] In a manner related to that of maximum lift (see the chapter on this subject) the lift-curve slope is also affect­ed (usually increased) by stream turbulence. For ex­ample (as reported by Millikan, CIT, around 1939) dC^/doGd 2412 increases from 0.094 (for 0.3% turbu­lence) to 0.105 (for 5.3% turbulence) at Rc = 1.4 (10)^.

.0! .o2 <03 -05*

Figure 22. Lift angle (15) ol toil sections as a function of minimum drag (friction and roughness).

—I—

Figure 23. The lift angle (15) of airfoil sec­tions as a function of Reynolds number, affecting their skin friction drag.

REYNOLDS NUMBER. Combining the last equation with a function expressing the section – drag coefficient for fully turbulent BTayer flow:

<W,„ – 0.1/R,/6 (14)

we can predict the variation of the lift angle at higher Reynolds numbers to be

A(da7dCL)»200 (t/c)/R/6 (15)

Some experimental results (reduced to two – dimensional coij&ition) as plotted in figure 23, confirm this expression at Renumbers above

[28]6. Below that number, serious variation can take place (due to BTayer transition) the character of which seems to depend upon the particular shape of the section nose.

B’LAYER TRANSITION. Growth andflowcon­dition of the boundary layer are a function of the Reynolds number (and of wind-tunnel tur­bulence). The character of the BTayer, whether laminar or turbulent, also depends upon the angle of attack. As a consequence, the Cl (o<) function is not always completely straight. Transition from laminar to turbulent BTayer flow may, for example, make the lift – curve slope slightly irregular, particularly at smaller R’numbers. We have, wherever this seems to take place, in the many graphs in this text, indicated discontinuities in the Cl(o<) function by not fairing a line through them, but by leaving the experimental results as discontinuous as they are found.

[29] High Lift, Low Drag Airfoils

a) Wortmann, The Quest for High Lift, AIAA 74-1018.

b) Nash-Webber, Motorless Flight Research, NASA CR-2315.

c) Althaus, Stuttgarter Profilkatalog I, U of Stuttgart 1972.

d) Liebeck, Airfoils for High Lift, J of А/С Oct 1973.

e) Hicks, Optimizing Low-Speed Airfoils, NASA TM X-3213

[30] High Performance Airfoils for General Aviation

a) McGhee, Characteristics of a 17% Airfoil, NASA TND-7428.

b) Wentz, Fowler Flap System, NASA CR-2443.

[31] Mechanism of, and penalties due to icing:

a) Gelder, Droplet Impingement, NACA TN 3839.

b) Bosoden, Aerodyn Characteristics, NACA TN 3564.

c) Gray, Penalties (Summary), NASA TN D-2166 (1964).

[32] At negative angles (negative camber):

a) NACA, In Variable Density Tunnel, TN 397 & 412.

b) AVA Gottingen, Ergebnisse III (1927) p 78, 79.

c) Williams, RAF-34 in CAT, ARC RM 1772 (1937).

[33] NACA “H” sections, for helicopter blades:

a) Stivers, Several Sections, W’Rpt L-29 (1946).

b) Schaefer, Between 9 and 15% Thick, TN 1922 (1949).

c) Stivers, 8-H-12 Section, TN 1998 (1949).

[34] “Laminar” airfoils for sailplanes:

a) Carmichael, Thick Foils, “Soaring” 1958 (Nov/Dec).

b) Wortman, Laminar Profiles, ZFW 1957 (May).

[35] Cascades of foils, vanes, blades:

a) Krober, Ingenieur Archiv 1932 p 516.

b) Patterson, Duct Corners, ARC RM 1773 (1936).

c) ARC, Tests, RM 1768; Analysis, RM 2095 & 2920.

[36] Principles and results of lifting-line theory:

a) Prandtls Wing Theory, Nachrichten Konigliche Gesellschaft Wi’schaften 1918 p 451, 1919 p 107.

b) Glauert, “Elements of Aerofoil and Airscrew Theory”, Cambridge University Press, 1926 and 1948.

c) Account of Lanchester’s work given by Prandtl “Generation of Vortices”, Paper RAS London, 1927.

[37] Analysis of trailing wing vortices:

a) Wetmore, Hazard For Aircraft, NASA TN D-1777; also Astronautics/Aeronautics, Dec 1964 p 44.

b) Kaden, Roll-Up Analysis, Ing Archiv 1931 p 140.

c) McCormick, Vortex Sheet, Penn U A’Engg 1965.

d) See AIAA J. 1963 p 1193; Aeron Quart 1965 p 302.

e) Mechanism of vortices (cores) by Newman, Aeron Quart 1959 p 149; Schaefer, J. Fluid Mech 1959 p 241.

f) Squire, Viscous Analysis, Imp Coll London (1954).

[38] Experimental results end plates and winglets

a) NACA Technical Rpts 201 and 267 (1927).

b) Riley, End-Plate Shape, NACA TN 2440 (1951).

c) Clements, Canted Plates, Aeron Eng Rev July 1955.

d) See due-to-lift chapter in “Fluid-Dynamic Drag”.

e) Riebe, On 45° Swept Wing, NACA TN 2229 (1950).

f) Wadlin, On Hydrofoil, NACA RM L1951B13.

g) Bates, H’Tail Surfaces, NACA TN 1291 (1947).

h) САНІ (Moscow) Technical Rpt 58 (around 1930).

i) Halliday, Very Large Plates, ARC CP 305 (1956).

k) Riley, Vertical With Horizontal Tail, NACA Rpt 1171.

j) Roberts, Drag Planer Wings USAACLABS TR 65-79

k) Whitcomb, Design and tests Winglets, NASA TN D-8260, 1976

l) Kirkman, Effectiveness Devices Tests, NASA CR-2202, Dec. ’73

m) Flechner, Second-Generation winglets, NASA TN D 8264 1976

n) Wentz, Wing-Tip devices N76 11012, July ’75

[39] Pressure distribution around foil sections:

b) Kochanowsky, Theoretical, Ybk D Lufo 1940 p 1-72.

a) Pinkerton, 4412 Distribution, NACA T Rpt 613.

[42] Airfoils with A = 6, tested in NACA FSTunnel:

a) Silverstein, Clark-Y Airfoil, T Rpt 502 (1934).

b) Goett; 009, 0012, 0018 Airfoils, T Rpt 647 (1939).

c) Bullivant, 0025 and 0035 Airfoils, T Rpt 708 (1941).

[43] Airfoils as tested in “large” DVL wind tunnel

a) Doetsch and Kramer, Lufo 1937 p. 367 and 480; also Yearbk D Lufo 1937 p. 1-69, 1939 p. 1-88 and 1940 p. 1-182.

b) Hoerner, Clark-Y Series, DVL Rpt Jf 208/3 (1940): also in small tunnel, FB 65 (1934).

c) Collection of DVL Results, ZWB FB 1621 (1943).

d) For DVL (and other) results see also reference 19.

e) Pressure Distributions, Ringbuch Luftf Tech I, A,11.

[47] Influence of stream turbulence:

a) Platt, Turbulence Factors, NACA T Rpt 5 58 (1936).

b) Dryden, Turbulence Companion of R’Number, J A Sci 1934 p. 67; also Wind Tunnel Turbulence, NACA T Rpts 320, 342, 392, 581 (1929/37).

c) Milliken, Turbulence Aircraft Engg 1933 p. 169; Max­imum Lift, ASME Trans 1934 p. 815.

d) Hoerner, Influence on Spheres, Lufo 1935 p. 42 (NACA Memo 777).

e) Dryden, Low-Turbulence Tunnels, T Rpt 940 (1949). 0 Jacobs, NACA VDT Tunnel, T Rpt 416 (1932).

[48] A variety of wing sections can be found in:

a) Ergebnisse AVA Gottingen, 4 volumes (1920/32).

b) Louden, Collection of Foils, NACA T Rpt 331 (1929).

c) ARC, RAF-34, RM 1071, 1087, 1146, 1635, 1708, 1772 (1927/37).

d) Characteristics of airfoil sections from all over the world, at lower or intermediate R’numbers, have been collected and presented in NACA T Rpts 93, 124, 182, 244, 286, 315 (1920 to 1929).

[49] Influence of roughness caused by icing:

a) Gerhardt, (AVA), Ybk D Lufo 1940 p. 1,575.

b) Bowden, Ice Formation, NACA TN 3564 (1956).

c) Gray, 65-212 Airfoil, NACA TN 2962 (1953).

[50] Lift at High Angles of Attack 0-180°:

a) Critzos, NACA 0012, oc-Q to 180°, NACA IN 3361.

b) Helicopter Model Blade Stall, J of AHS, Jan 1972.

c) Sike and Gorenberg, 63A, oC – 0 to 180° AVLABS TR 65- 28, AD 619153

[51] Particularly thick airfoils with flaps:

a) Wenzinger, 23021 With Slotted Flaps, NACA TRpt 677 (1939).

b) Duschik, 23021 With 40% Slotted Flap, NACA TN 728 (1939).

c) Recant, 23030 Airfoil With Various Slotted Flaps, NACA TN 755 (1940).

d) Harris, Pressure Distribution With Slotted and Split Flap, NACA TRpt 718.

e) Harris, 23012/30 Airfoils With Slotted Flaps, NACA TRpt 723 (29,a) (1941).

f) Wenzinger, 23012/30 Airfoils With Split Flaps, NACA TRpt 668 (15,b) (1939).

[52] Airfoils with slats and trailing-edge flaps:

a) Seiferth, High-Lift Airfoils, Yearbk D Lufc 1939 p 1-84.

b) Lyon, High-Lift Devices, ARC RM 2180 (‘.939).

c) Schuldenfrei, 23012 With Slat and Flaps, NACA WRpt L-261 (1942).

* САНІ SECTION WITH 30° SLOTTED FLAP (3,a)

О SAME COMBINATION IN WATER TUNNEL 106 (3,b)

* 23012 W’ MAXWELL SLAT AT 2(10 )6 (6,b, C)

[54] (WITH AND WITHOUT 204/60° SPLIT FLAP)

X CLARK-Y W’ MAXWELL SLAT AT 6(10)5 (6,a)

x (WITH AND WITHOUT 20%/60° SPLIT FLAP)

Л BRITISH EQ-1040 SECTION AT 9(10)5 (5,e)

Л (WITH AND WITHOUT 204/60° SPLIT FLAP)

О RAF-31, WITHOUT TRAILING FLAP (5,g)

Figure 7. Maximum lift coefficients as a function of the slat-chord ratio.

[55] Investigation of so-called Kruger flaps:

a) Kruger, Laminar Wings with Nose Flaps, ZWB FM-1148 (1944);

b) Kruger, Mustang Airfoil (including pressure distributions) ZWB UM-3153 (1944); see NACA TM 1177.

c) Riegels, Russian Airfoil, ZWB UM-3067 (1944); see NACA TM 1127.

d) Fullmer* 64-012 Airfoil With Kruger Flaps, NACA TN 1277 (1947).

[56] Boundary-layer control of nose flaps by suction:

a) Holzhauser, Airplane With Flaps and BL Control, NACA RM A1957K01.

b) Koenig, Wing Fuselage With Flaps and Suction, NACA RM A1956D23.

c) There are many wind-tunnel results available, dealing with flaps and boundary-layer control on swept wings such as NACA RM A1953J26, A1955K29, A1956F01, A1957H21. Some information on such wings is presented in the “swept wing” chapter.

d) Holzhauser, Tunnel and Flight Tests on a 35 Swept Wing With Leading-Edge Suction Flap, NACA TRpt 1276 (1956).

[57] Hoerner, Maximum Lift by Blowing, ZWB (DVL) FB-276/1&2 (1935).

[58] Munk, Comments on Velocity of Sound, J. Aeror Sci 1955 p Figure 1. Propagation of pressure disturbances in a compressible 795. fluid in relationship to operating speed.

[59] Pressure distribution and lift of airfoils as a function of M’number:

a) von Doenhoff, Cambered at Low Speed, NACA TN 1276 (1947).

b) Wall, Chordwise Distribution, NACA TN 1696 (1948).

c) Cooper, Testing the Same Wing as in (a), NACA TN 3162 (1954).

e) McCullough, 10% Sections Cambered at Low Speed, NACA TN 2177 (1950).

f) Graham, Five Airfoil Sections, NACA Rpt 832 (1945).

g) Goethert, OOXX Series, ZWB FB-1505 (1941); see Cana­dian Nat Res Laboratories Trans TT-25, 26, 27, 28, 29 (1947).

h) Nitzberg, Evaluation of (f) and (g), NACA TN 2825 (1952).

i) Tapered Wing, Original DVL Graphs Jf-712 (1944).

[60] Characteristics of wings as a function of Mach Number:

a) Nelson, 36 Different Wings on Bump, NACA TN 3529

(1955).

b) Hamilton, 6 Wings 65-Series Airfoils, NACA Rpt 877

(1947).

c) Nelson, 22 Rectangular Wings on Bump, NACA TN 3501

(1955).

d) West, 64-210 Tapered Wing, NACA TN 1877 (1949).

e) Nelson, 38 Cambered Wings on Bump, NACA TN 3502

(1955).

f) Polhamus, 65A Series with A = 2 and = 4, NACA TN 3469

(1955).

[61] Diederich (NACA), analysis of lift as a function of A’ratio

and M’number:

a) Correlation on the Basis of “F”, TN 2335 (195 1 ).

b) Spanwise Lift Distribution (Flaps), TN 2751 (1952).

[65] Characteristics of flaps and control surfaces:

a) Knappe, Heinkel Tunnel Tests, Yearbk D Lufo 1941 p 1-96.

b)Tinling, Horizontal Tail Surface, NAC’A RM A19^9Hlla.

[66] Hydrodynamic characterіstіc-s~ ofv>hip mdders:

a) Hagen, TMB Rpt C-398; also C-125 & 373 (I 951).

b) Jaeger, Torque 8c Pressures, J. Shipb Progr 1955 p 243.

c) Thiemann, In Wind Tunnel, Schiff & Hafen 3962 p 42.

d) The 0015 section with various flaps (rudders) in NACA Wartime Rpts L-378, L-448, L-454 (1942).

[67] Rudder forces and turning of ships:

a) Davidson, Turning 8c Steering, Trans SNAM E 1944/46.

b) Becker 8c Brock, Trials, Trans SNAME 1958, p 310.

c) Mandel, Appendages, Trans SNAME 1953 p 464.

[68] Control Surfaces with flaps, for ships or boats:

a) Windsor, 0015, Univ Md Tunnel Rpt 268 (1959).

b) Bowers, for submarine application, see (9,a).

c) White, Rudder in W’Tunnel, TMB Rpt 1231 (1958).

d) Bates, Collection Tail Surfaces, NACA TN 1291.

[69] Analysis of small aspect ratio wings:

a) Polhamus, Low A’Ratio Wings, NACA TN 3324.

b) Bartlett, Shape of Edges, J Sci 1955 p 517.

[70] Information on modern submarines:

a) McKee, Design Practices, SNAME Paper 11, 1959.

b) Submarines & Destroyers, The Engineer Jan 1962.

c) Control, by McCandliss in IAS Paper 1961-45,

d) Malloy, Aircraft Techniques, IAS Paper 1961-42.

[71] Control surfaces designed for submarines:

a) Bowers, on Simulated Hull, U Md Tunnel Rpt 259.

b) Harper, 0015 Hull, Georgia Inst Tech 1959.

c) Some “surfaces” under (1) for submarines?

[72] An exception are the tests in (15,c).

[73] NACA, Fully Submerged Hydrofoils Tested:

a) Benson к Land, Foils in T’Tank, W’Rpt L-757 (1942).

b) Wadlin, Aspect Ratio 10, RM L9Kl4a (1950).

c) Wadlin-Ram-Vaug, Flat Plates, Rpt 1246 (1955).

d) Wadlin-Shuf-McGeh, Also Theory, Rpt 1232 {1955).

e) See references (15,d) and (17,a).

[74] Fully-submerged hydrofoils (with struts):

a) Kaplan, With A = 6, Stevens ETT Letter Rpt 428.

b) Ripken, 16-509, Univ Minn SAF Lab Rpt 65 (1961).

c) Feldman, 6 Hydrofoils in Tank, DTMB Rpt 1801.

d) Wadlin, End Plates Struts, NACA RM L51B13; see (11,d).

e) Hoerner, Struts-Nacelles, G&C Rpt 14 (1953).

f) Jones, Various Foils, Convair Rpt ZH-146 (1960).

[75] Characteristics of small-aspect-ratio hydrofoils:

a) Wadlin, Rectangular Flat Plates with A =- 0.125, = 0.25, – 1.0; NACA Rpt 1246, TN 3079 & 3249 (1954).

b) Ramsen, Strut Interference, NACA TN 3420 (1955).

c) Vaughan, Plate to 80 ft/sec, NACA TN 3908 (1957).

d) Vaughan, Hydroskis, NASA TN D-51 &: D-166 (1959).

[76] Influence of control flaps upon hydrofoils:

a) Jones, 16-309 With Flaps in Towing Tank,

Convair Rpt ZH-153 1961; AD-268,233.

b) Conollv, Review of Hydrofoils, J Aircr 1965 p 443.

c) Conolly, Flaps in Waves, Convair Rpt GDC-1953-032.

[77] Experimental characteristics of hinged flaps:

a) Silverstein, Horizontal Tail Surfaces, NACA T Rpt 688 (1940); also J Aeron Sci 1939 p 361.

b) Ames and Others, 0009 Pressure Distributions, NACA TN 734, 759, 761 (1939/40), see (2,e).

c) Gothert, Systematic Investigations, ZWB

FB 552 к 553 (1938/40);Yearbk D Lufo 1940 p 1-542.

d) Gothert, Horizontal-Tail Characteristics,

Ringbuch Luftfahrt Technik (Chap I-A-13, 1940).

e) Ergebnisse AVA Gott, Vol. Ill (1926) p 102.

f) Dods, A’Ratio and Sweep, NACA TN 3497 (1955).

g) Wenzinger, Wing Flaps, NACA TR 554 (1936).

h) Irving, Elevators, ARC RM 679 (1920).

i) Jacobs, Pressure Distrib., NACA T Rpt 360 (1930).

j) Polish Results, see (4,d) also NACA TR 688.

k) NACA, Report/Memorandum L1948D09.

l) Glauert, ARC RM 761 (1921) & RM 1095 (1927).

m) Abbott-Doenhoff-Stivers, NACA TR 824 (1945).

n) Swanson, Tail Surface, NACA TN 1275 (1947).

o) Spearman, With 25 к 50% Flaps, NACA TN 1517.

[78] The span ratio bp/b is taken into account in these cases. In presence of a fuselage, “b” of a horizontal tail is to be measured from tip to tip, while the span of the elevator is usually reduced either by a cut-out or corresponding to the width of the fuselage.

[79] Truckenbrodt, Flapped Delta Wing, ZFW 1956 p 236.

[80] It is general practice in tunnel testing to correct the angle of attack for boundary effects of the wind stream, A corresponding correction (likely in proportion to dcx/d<S ) should be applied to the flap angle. We have, wherever possible, used uncorrected tunnel-tested val­ues for the angle of attack.

[81] Flaps on swept-back wings:

d) Harper, NACA TN 2495 (1951); (18,d) (22,c).

e) Letko, Swept-Back Wings, NACA TN 1046 (1946).

f) Dods, Horizontal Tails, NACA TN 3497 (1955).

g) Dods, Swept-Wing Theory, NACA TN 2288 (1951).

[82] In the discussion of flap characteristics as a function of aspect ratio, derivatives considered are those at and around zero lift. At aspect ratios approaching zero, a

non-linear, “second” term of lift originates as a func­tion of the angle of attack or when deflecting a trailing – edge flap.

[84] Influence of foil section shape:

a) Lockwood, Beveled, NACA W Rpt L-666 (1944).

b) Jones, Beveled Trailing Edge, NACA WR L-464.

c) See Harper (18,d), Various Foil Sections.

d) Batson, 0015 Modified, ARC RM 2698 (1943).

e) Halliday, Rudder Moments, ARC RM 2184 (1941).

f) Sears, Flap and Tab, NACA WR L-454 (1942).

g) Toll, Surface Distortion, NACA TN 1296 (1947).

h) Toll, Lateral Control, NACA T Rpt 868 (1947)

i) Crane, Modifications, NACA T Rpt 803 (1944).

j) Hemenover, T’Edge Angle, NACA TN 3174 (1954).

k) Halliday, Boundary Layer, ARC RM 2730 (1955).

l) ARC, Flaps, RM 1996, 2008, 2256, 2506 (1942/45).

[85] Characteristics of flap-plus-tab systems:

a) For theory5see references (2,b) and (2,e).

b) For results, see references (4,b) and (4,d).

c) Harris, Moments due to Tabs, NACA T Rpt 528.

d) Wenzinger, Pressure Distrib., NACA T Rpt 374.

f) Bausch, Wing, Yearbk D. Lufo 1940 p.1-182.

g) Crandall, Correlation, NACA TN 1049 (1946).

h) Brewer, Balanced Tabs, NACA TN 1403 (1947).

i) 0015 with Flap and Tab, ARC RM 2314 (1943).

[87] For tab-chord ratios exceeding 0.2, interpola­tion by dC^/d^ V C|/Cj. would be better.

[88] Note that the hinge moment due to lift (at fixed flap angle) is not affected by a tab.

[89] Characteristics of linked-tab balance:

a) Harper, Tail Surfaces, NACA TN 2495 (1951).

b) Dunn, DC-6 Airplane Control Surfaces, Proc Internat Aeron Conf IAS/RAS, New York 1949.

c) Balancing Tabs, ARC RM 2510 (1941).

[90] Stiess, Influence of Linked-Tab Upon Stability and Control, Yearbk D. Lufo 1941 p.1-252.

[91] McKee, H’Tail Leading Tab, NACA WR L-702 Ц943).

[92] Characteristics of servo-tab control:

a) ARC, Rudders, RM 1105 & 1514 (1927/32).

b) Reid, Servo Control, J Aeron Sci 1934 p. 155.

c) Wright, Servo-Control, ARC RM 1186 (1928).

d) ARC, Servo Ailerons, RM 1262 (1929).

[93] Steering machinery including accessories of an ocean liner may weightwise be in the order of 20 tons. This much may only be 0.1% of the vessel’s displacement weight, however.

[94] Reid (38,b) reports that between 1921 and 1926 some 25 sea-going ships were equipped with servo-tab rud­ders. He also reports that between 1926 and 1934 a number of larger British airplanes were using servo rudders.

[95] Investigation of spoiler-type devices by the NACA :

(a) Weick, Rolling Moments Obtained, NACA IN 415 (1932).

(b) Weick, Ailerons and Spoilers, NACA T Rpt 494 (1934).

(c) Weick, Slots and Spoilers, NACA TN 443 (1933).

(d) Shortal, Location and Effects, NACA TN 499 (1934).

(e) Shortal, Slot-Lip Ailerons, NACA T Rpt 602 (1937).

(f) Sou(e, Flight Investigation, NACA T Rpt 517 (IS 35).

(g) Wetmore, Retractable Ailerons, NACA TN 714 (1939).

(h) Wenzinger, NACA TN 801 and T Rpt 706 (1941).

(i) Rogallo, Plug-Type Aileron, NACA Wr Rpt L-376 & 420 (1941).

(j) Spahr, Flight Investigation, NACA W Rpt A-28 (3943).

(k) Spohr, Flight Investigation, NACA TN 1123 (1947).

(l) Fishel, Location of Spoiler, NACA TN 1294 (19^-7).

(m) Deters, With Full-Span Flaps, NACA TN 1409 (1 947).

(n) Schneiter, On Swept Wing, NACA TN 1646 (19z-3).

(o) Fishel, Retractable Ailerons, NACA T Rpt 1091 (1952).

(p) Fishel, Collection of Data, TN 1404 (1948).

(q) Wenzinger, Lateral Devices, NACA TN 659 (1958).

(r) NACA, T Notes 1015,1245,1409,3705,4057.

[96] Differential-linkage balancing of ailerons:

(a) Weick, Rigged-Up Ailerons, NACA T Rpt 423 (1932).

(b) Differential Linkages, NACA TN’s 586 & 653 (1936/38).

(c) Differential Gearing, ARC RM 2526 (1940).

[98] The subscript n as in equation (16) indicates the vertical or normal axis of the airplane, about which the yawing moment is defined.

[99] Compensation for CDS, – Diehl (l, b) recommends a value of 0.15. The corresponding factor in equation 12 is 0.30.

[100] “Cross flow” and “upwash” are covered in connection with

Chapter IX on the “horizontal tail”, Chapter XII on “engine nacelles”, and Chapter XIX on “streamline bodies”.

[102] Contribution of fuselage to longitudinal moment;

a) Vandrey, Analysis, Yearbk D Lufo 1940 p 1-367.

b) Jacobs, 209 Combinations, NACA T Rpt 540 (1935).

c) Sherman, Interference of Wing-Fuselage Combinations, NACA T Rpt 575 (1936); and TN 1272 (1937); see also TN 641 & 642 (1938) for special junctures.

d) Liebe, Theoretical Analysis, Ybk D Lufo 1942 p 1-280.

e) Moller, Ybk D Lufo 1942 p 1-336; also ZFW 1953 p 2.

f) Yates, Flying Boat Hulls, NACA TN 1305 (1947).

[103] See “Fluid-Dynamic Drag”, Chapter VIII, under “induced interference drag”.

[104] Influence of wing shape on downwash:

a) Crowe, Tapered Wings, Aircr Engg March 1937 p 59.

b) Muttray, Cut-Out, Lufo 1935 p 28 (NACA TM 787).

c) Schulz, Plan-Form Analysis, Lufo 1942 p 367.

[105]

[106] Interference of wing wake upon horizontal tail:

a) Ruden, Study, Ybk D Lufo 1939 p 1,98 & 1940 p 1,204.

b) Walter, Interference, J Aeron Sci 1938 p 300.

c) White, Wing-Fuselage Interference, NACA T Rpt 482 (1934).

d) Lieblein, Wake Characteristics, NACA TN 3711 (1956).

e) Spence, Wake Behind Foil, ARC CP 125 (1952).

f) See Silverstein in NACA T Rpt 651 (17,d).

[107] Ankenbruck, Comparison of Performance, Conventional/- Tailless/Tail-Boom, NACA TN 1477 (1947).

[108] Underslung Engines – V/ing Augmentation:

a) Parlett, Wind-Tunnel Test Jet Transport with External – Flow Jet Flap, NASA TN D-6058.

b) Powers, Experimental STOL Configuration with Ex­ternally Blown Flap Wing or Augmentor Wing, NASA TN D-7454.

c) Patterson, High-Bypass Engine Wing-Nacelle Interference Drag, NASA TN D-4693.

d) Parlett, STOL Model with Externally Blown Jet Flap, NASA TN D-7411.

e) Zabinsky, STOL Designs for NASA Short Haul Transport Study, NASA SP-116, P-339.

[109] Influence of propeller slipstream on downwash:

a) Stuper, Slipstream on Tail, Lufo 1938 p 18.1 (NACA TM 874).

b) ARC, Downwash in Slipstream, RM 882 (1924).

c) Katzoff, Slipstream Effects, NACA T Rpt 690 (1940).

d) Helmbold, Airplane Model, Lufo 1938 p 3.

e) Muttray, Distribution, Lufo 1938 p 109 (NACA TM 876). (12) Downwash behind isolated propellers:

0 In biplane configuration, ARC RM 1488. a) Glaurert, ARC RM 882; see Durant IV p 357.

g) Goett, Pitching Moments, NACA W’Rpt L-761. b) Turin, Experimental, J Roy A Soc 1936 p 388.

[110] Influence of single propeller on stability, experimental:

a) Goett, Tilted-Engine Axis, NACA T Rpt 774 (1944).

b) Priestley, Fighter Airplanes, ARC RM 2732 (19.53).

c) Recant, Pursuit Model, NACA W Rpt L-710 (1942).

d) Weil, Curtiss BTC-2, NACA W Rpt L-667 (1944).

e) J Aeron Sci, High Wing, 1936 p 73; Low Wing, 1937 p 411.

f) Wallace, Influence on Low Wing, NACA TN 1239 (1947).

g) Purser, Unsymmetrical Horizontal Tail, NACA TN 1474 (1947).

[113] Airplane models with running propeller:

a) Stuper, Collection of Data, Ringb Luftf Technik IA12 (1939).

b) He-70 and AR-196, tested at AVA, are included in (a).

c) Hoerner, “Fi-157” in DVL Tunnel, Fieseler Rpt April 1937.

d) Weil, 29 Configurations, NACA TN 1722 (1948); T Rpt 941.

[115] Contra-rotation in twin-engine airplanes:

a) Engines or propellers rotating in opposite directions are undesirable with respect to fabrication and number of spare parts to be kept available.

b) Seiferth, In Wind Tunnel, Ybk D Lufo 1938 p 1-220.

c) Stiess, Do-17 in Flight, Ybk D Lufo 1938 p 1-206.

(1938).

[117] Directional characteristics of engine nacelles:

a) Fournier, “Exotic” Configuration, NASA D-217 (1960).

b) Pabst, FW-200 Airplane, Focke Wulf Wind-Tunnel Rpt 41

[120] Lateral stability and control characteristics:

a) Schlichting, Interaction Between Wing Fuselage and Tail Surfaces, Ybk D Lufo 1943 Rpt IA028.

b) McKinney, Lateral Stability, NACA TN 1094 (1946).

c) Maggin, Swept Model Flight Tests, NACA TN 1288

(1946).

d) Michael, Fuselage V’Tail Interaction, TN 3135 (1954).

[121] Sidewash induced by wing and fuselage:

a) Bamber, Wing + Fuselage + Fin, NACA TN 730 (1939).

b) House, Wings Fuselages Fins, NACA Rpt 705 (1941).

c) Recant, Side Flow at V’Tail, NACA TN 804 & 825 (1941).

d) Schlichting, Wing & Fuselage, Ybk D Lufo 1941 p. 1-300.

e) Sweberg, Load on V’Tail, NACA W’Rpt L-426 (1944).

f) Goodman, Wing and H’Tail, NACA TN 2504 (1951).

[122] Characteristics of “V” tail surfaces:

a) Purser, Simple Vee-Tail Theory, NACA T Rpt 823 (1945).

b) Schade, Isolated Vee-Tail Surfaces, NACA TN 1369

(1947) .

c) Polhamus, Airplane with Vee Tail, NACA TN 1478

(1947).

[123] Twin-engine airplanes, flight-tested:

a) Sjoberg, Douglas A-26, W’Rpts L-606, 607, 608 (1945).

b) Crane, DeHavilland “Mosquito”, W’Rpt L-593 (1945).

[124] That difference can be important, however, when considering larger angles of attack, such as in stalled and/or spinning conditions.

[125] Tunnel-tested characteristics of straight wings:

(a) Bamber, Plan Forms, NACA TN 703 & 730 (1939).

(b) British ARC, Reports RM 394, 1059, 1203, 2019.

(c) Blenk, Dihedral Sweep Twist, Lufo 1929 p 27.

(d) Zimmerman, Small Aspect Ratios, NACA TRpt 431 (1932).

(e) Shortal, Shape and Dihedral, NACA TR 548 (1935).

(f) Doetsch, 6-Component, Yearbk D Lufo 1940 p 1-62.

(g) AVA Gottingen, results. quoted by Seifirth (5,d).

(h) Moller, Rectangular Wings, Lufo 1941 p 243.

(i) Results from AVA Gottingen, see (5,d).

(j) Hansen, Elliptical Wings, Ybk D Lufo 1942 p 1-160.

.(3) The smallness of the lateral forces is also the reason for the scatter of the experimental points in figure 3.

[126] Influence of wing flaps on lateral characteristics:

(a) Teplitz, Configuration w’Flaps, NACA TR 800 (1944).

[127] Lateral characteristics of wing-fuselage configurations:

(a) Moller, 6-Component Results, Ybk D Lufo 1942 p 1-336.

(b) Bamber, Wing, Fuselage & Fin, NACA TN 730 (1940).

(c) Schlichting, Review of Subject, Ybk I) Lufo 1940 p 1-113.

[128] Lateral Stability Theory:

(a) Babister, A. W., Aircraft Stability and Control, Pergamon Press 1961.

(b) Stemfield, L., Dynamic Stability, NACA University Conf 1948.

(c) Perkins & Hage, Airplane Performance Stability and Con­trol, John Wiley & Sons,’ 1949.

(d) Campbell & McKinney, Calculating Methods Dynamic Lateral Stability, NACA TR 1098.

[129] Predicting spanwise loading of swept wings:

a) Weissinger, Original Method (1940), NACA TM 1120.

b) Multhopp, Lifting-Surface, Brit RAE Rpt Aero 235 3.

c) Schneider, Comparison/Experiments, NACA Rpt 1208.

d) Kuchemann, Calculated Distribution, ARC RM 2935.

e) Toll, Stability Derivatives, NACA TN 1581.

0 DeYoung, For Arbitrary Plan Form, NACA Rpt 921.

g) Van Dorn, Comparison of Methods, NACA TN 1476.

h) Falkner, On 3 Wings A = 6, ARC RM 2596 (1952).

[130] The function for sharp rectangular wings as described in the text, corresponds to a – 0.9 and ^b/c = 0; while that for “round” wings is obtained for a = 0.9, (дЬ/с) =-0.2, and ДЬ/с = -0.2/ &1 + 2/A3 , while дЬ/Ь = (ДЬ/с)/А and к = f(“A”) as in figure 1, where A • = A + ab/c. Note that the latter line ends below A = 1 in a constant lift ratio of 0.8 as against that of the sharp-rectangular wings.

a 1 U

[132] 5 6

Figure 19. Correction to Prandtl-Glauert compressibility equa­tion for aspect ratio.

Where M i_ B is the Mach number where the force break occurs and M L m is the Mach number at the

minimum lift slope. The reduction in slope at M |_ m is a function of thickness and aspect ratio and can be estimated using figure 22. It is noted that when the thickness ratio of the wing is below 5% low aspect ratio wings do not exhibit a reduction in lift slope.

[133] Analysis considering delta wing vortex formation:

a) Legendre, Recherche Aeronautique No. 30, 31. 35 (1952/53).

b) Brown, “Separation”, NACA TN 3430 and J Aeron Sci 1954 p 690.

c) Chang, Non-linear Lift, J Aeron Sci 1954 p 212.

d) Jones, NACA T Rpt 835 (1946); also J Aeron Sci 1951 p 685.

e) British Efforts, ARC RM 1910, 2596, 2819, 3116.

f) NACA, Wing Theory, T Rpts 921 & 962 (1948/50)

g) Lomax, Slender Wing Theory, NACA T Rpt 1 105 (1952).