Reduction of level flight performance data

It has been already been shown that the power required by a helicopter can be written in terms of referred groups as:

p = Уw V V Z _ш

aw3 lam2’ m’m’ ’VqJ

P = УW V V Z _m_

§7Q 5 , m, m ’ ’7ё/

In level flight, Vc = 0 and generally the aircraft will be outside ground effect. Thus:

P = УW V _m

aw3 I am2’ m ’ VQ!

P = У W V _m_

5V9 5 m VQ/

It is interesting to compare the latter relationship with the power coefficient formula reviewed earlier:

1 f 1

CP = 1.2XCT + 2 V A + – v(1 + 4.3^2 )CD + CPm + CPs

It has already been shown that X = f(p). Additionally it can be surmised that the power increment due to retreating blade stall will be a function of rotor speed and forward speed (advance ratio) hence CPs = f(p). Also the power loss due to com­pressibility will depend on rotor speed, forward speed and Mach number, so CPm = f(p, MB). Thus, the power coefficient formula can be written as:

CP = f(CT, p, MB)

Noting that for a given helicopter:

^ P P P

CP Л тлЗ ё r3 ё З

pAV 3 p )3 am3

„ T w w

CT ЛТ/2 ё n2 ё 2

pAV 2 p )2 affl2

V V V

P = — ос— ё — Vt ) m

The direct correlation between performance expressed in coefficient terms and perfor­mance expressed using referred parameters can be seen readily.

Since SFC is rarely constant with power it is necessary to document the variation of referred fuel flow rate with referred TAS, referred weight and referred rotor speed

Fig. 3.12 Variation of referred fuel flow with referred TAS – test data.

to determine the endurance performance. Since the fuel flow rate of a gas turbine engine will be dependent on the power generated it can be assumed that G = f(P). Thus referred fuel flow is directly related to referred power:

G = Jw V _m_

am3 Uffl2’m ’ Vq)

G = JW V _m

s Vq | s m Vq/

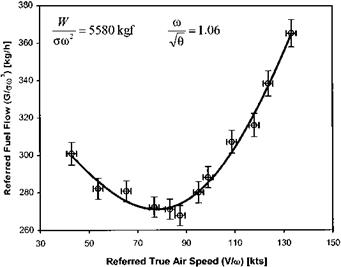
Figure 3.12 shows a typical variation of referred fuel flow (G/am2) with VIm for a single value of Wlam2 and ml-VQ.

Likewise, it is necessary to document how referred specific air range varies with referred weight, referred true airspeed and referred rotor speed. Since SAR is equal to the ratio of true airspeed and fuel flow, their referred forms can be used in order to find the referred form of specific air range. Thus:

= f(W V _m________ =f(W V m _L = JW V m 1

Fig. 3.13 Variation of referred SAR with referred TAS – test data. and:

cad s A w V m

SAR 8 = f —r, —, ^

offl2 m V6/

Figure 3.13 shows a typical variation of referred SAR (SAR 8) with V/m for a single value of Wlam2 and m/^0.