Effect of aero-derivatives on dynamic stability modes

The dynamic response of a helicopter is governed by the values of the aerodynamic and control derivatives that make up the characteristic equation and stability matrices. Most of the important derivatives are speed dependent so it will be instructive to examine the variation in the dynamic modes with airspeed as well as determining the effect of modifying single derivative values.

4.9.7.1 Effect of airspeed

Some idea of the likely behaviour can be obtained by examining the aero-derivative and control matrices. Below are a set of matrices for three flight cases: hover, 60 KTAS and 120 KTAS.

– 0.0253	0.0215	0.6675	– 9.7838
0.0276	– 0.3120	0.0135	– 0.7215
0.0482	0.0051	– 1.8955	0
0	0	0.9986	0
6.9418	– 9.2861
– 93.9176	– 0.0021
0.9554	26.4011
0	0
– 0.0243	0.0392	– 0.6705	– 9.8014
– 0.0467	– 0.7285	30.8626	– 0.4200
0.0280	0.0248	– 2.2189	0
0	0	0.9995	0

Ahov

Bh0v —

A60 —

4.6289	– 8.0560
– 107.3895	– 21.2286
10.7004	27.6889
0	0
– 0.0460	0.0385	2.7192	– 9.8052
0.0221	– 0.9008	61.5403	0.3205
0.0299	0.0380 –	2.6060	0
0	0	0.9989	0
3.8024	– 7.0223

B60 —

A120 —

– 135.2501 – 49.3052

20.9344 30.9867

0 0

The dynamic stability of the helicopter can be assessed by studying the eigenvalues of the A matrix. The eigenvalues equate to the solutions of the differential equations that underpin the matrix itself. Recalling that a negative real part is indicative of a convergent response and that a pair of complex roots imply an oscillatory motion we are in a position to describe the dynamic modes:

(1) Hover. The eigenvalues of the Ahov are:

0.0548 + 0.4805г, 0.0548 – 0.4805г, – 0.3142, – 2.0282

These eigenvalues imply an unstable second-order dynamic mode and two stable first-order responses. The second-order mode has a natural frequency of 0.484 rad/s (period of 13.0 s) and a relative damping value of — 0.1133 (T2 of 12.6 s). The first-order responses have time constants of 3.18 s ( — 0.3142) and 0.49 s ( — 2.0282).

(2) 60 KIAS. The eigenvalues of the A60 matrix are:

0.0735 + 0.3822г, 0.0735 — 0.3822г, — 0.4725, — 2.6460

These eigenvalues imply an unstable second-order dynamic mode and two stable first-order responses. The second-order mode has a natural frequency of 0.389 rad/s (period of 16.2 s) and a relative damping value of — 0.1885 (T2 of 9.4s). The first-order responses have time constants of 2.12s ( — 0.4725) and 0.38 s ( — 2.6460).

(3) 120 KIAS. The eigenvalues of the A120 matrix are:

0.1995 + 0.3784г, 0.1995 — 0.3784г, — 0.4191, — 3.5326

These eigenvalues imply an unstable second-order dynamic mode and two stable first-order responses. The second-order mode has natural frequency of 0.428 rad/s (period of 14.7 s) and a relative damping value of — 0.4664 (T2 of 3.5 s). The first-order responses have time constants of 2.39s (—0.4191) and 0.28s ( — 3.5326).

The period of the oscillatory mode is fairly long and this would be called the long­term dynamic mode which characterizes the dynamic stability. Therefore this helicopter is dynamically unstable and the degree of instability increases with speed.

4.9.7.2 Effect of increased pitch damping

The effect of an increase in pitch damping, achieved by a direct increase in the value of the pitching moment due to pitch rate (Mq), can be easily shown by increasing the appropriate value in the A matrix. Suppose that the value of Mq is doubled from — 2.505 to — 5.212:

" — 0.0460	0.0385	2.7192	— 9.8052
0.0221	— 0.9008	61.5403	0.3205
0.0299	0.0380	— 5.2120	0
0	0	0.9989	0

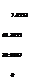3.8024 —

— 135.2501 —

20.9344 0

The effect of this change on the dynamic response of the helicopter can be seen from the change in the eigenvalues:

(1) Before. 0.1995 + 0.3784г, 0.1995 — 0.3784г, — 0.4191 and — 3.5326, which result in the following engineering parameters:

£ =— 0.4664, mn = 0.428 rad/s, T1 = 2.39 and T2 = 0.28

(2) After. 0.0501 + 0.2916г, 0.0501 — 0.2916г, — 0.5411 and — 5.718, which result in the following:

£ =—0.1693, mn = 0.296 rad/s, T1 = 1.85 and T2 = 0.17

This suggests that increasing Mq will reduce the frequency of the long-term mode and shorten the time constant for the short-term mode (control response).