LATERAL/DIRECTIONAL DYNAMIC STABILITY AND CONTROL RESPONSE

As with the longitudinal axis the lateral/directional dynamic stability of a helicopter is evaluated by observing the longer-term response to a disturbance. The aircraft will be dynamically stable if, following the removal of a disturbance force, it has a tendency to return to the trimmed attitude. Equally control response is again concerned with the response of the helicopter to control inputs made by the pilot. The analysis of the motions is simplified by assuming that there are no cross-coupling effects. Once again the reader should be reminded that this assumption is of questionable validity and care must be taken when reading-across the theoretical results, mentioned below, to the behaviour of an actual aircraft. Before looking at the dynamic modes in detail, it is worth reminding ourselves of the aero-derivatives that influence the lateral/directional motion.

4.11.1 Lateral/directional derivatives

4.11.1.1 Sideslip derivatives

Mechanisms for the generation of sideforce, rolling moment and yawing moment as a result of a lateral velocity disturbance have already been discussed.

4.11.1.2 Roll rate derivatives

(1) Sideforce due to changes in roll rate (Yp). The sideforces produced at the fin, the fuselage and the tail rotor due to changes in the relative airflow direction (and that due to the main rotor flapping) in a roll are generally negligible. This derivative is therefore normally ignored.

(2) Rolling moment due to roll rate (Lp). The main rotor contribution to roll rate damping is analogous to the pitch rate damping (Mq) discussed above. This aerodynamic damping effect is a function of Lock number and the size of the hinge offset. Smaller contributions are also provided by the tail rotor, the fin and the fuselage.

(3) Yawing moment due to roll rate (Np). Contributions to Np depend largely on the size and position of the tail rotor and fin. A high tail rotor, for example, would have a considerable effect, see Fig. 4.20.

4.11.1.3 Yaw rate derivatives

(1) Sideforce due to changes in yaw rate (Yr). It is present but considerable self­cancelling occurs due to effects fore and aft of CG. Yr is therefore usually small enough to be negligible.

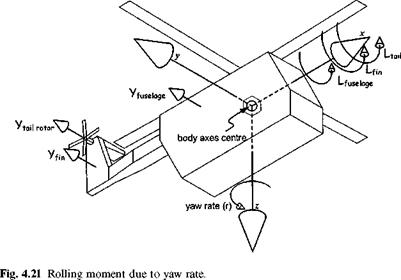
(2) Rolling moment due to yaw rate (Lr). The yaw rate produces a change in the direction of the relative airflow to the fin and tail rotor in particular. The sideforces produce a sizeable rolling moment if their lines of action are sufficiently

high above the rolling axis, see Fig. 4.21. If the rotor shaft is at an appreciable angle to the vertical, the main rotor may also provide a contribution to the rolling moment.

(3) Yawing moment due to yaw rate (Nr). If a helicopter yaws to starboard the tail rotor appears to be sideslipping to port. A blade element then experiences relative airflow from a direction that will effectively increase its angle of attack. There will be an associated increase in thrust and this will produce a damping moment opposing the yaw rate. The effect is present in both the hover and
forward flight. A starboard yaw rate also produces relative airflow to both fin and fuselage which gives rise to a net sideforce from each surface. Both associated moments make stabilizing contributions to Nr.