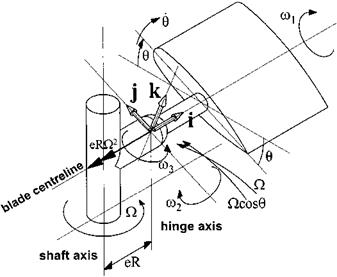
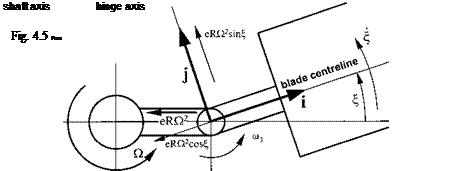
Pure lead/lag motion

Since a flapping blade is likely to move in the lead/lag sense it is necessary to determine whether the lead/lag motion will cause any rotation about the other two axes. It is now assumed that the flapping angle is zero and the blade moves forward on the drag hinge through an angle E, as in Fig. 4.5. In this case:

m1 = 0 m2 = 0 m3 = ) + E

ax = — )2eR cos | ‘і

ay = )2eR sin | I (4.14)

az = 0 J

and making the appropriate substitutions (Equations (4.13) and (4.14) into Equation (4.9):

L = 0 M = 0

N = Izz | + mbXgeR2 )2 sin | J

Thus when a rotating blade moves solely in a lead/lag sense no moments are generated that cause additional flapping or feathering motion.

4.4.2 Pure feather motion

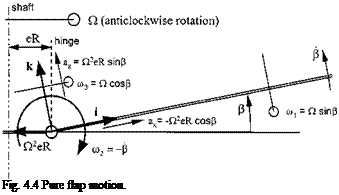
As shall be seen later it is necessary to feather a rotor blade if changes in disk tilt and/ or thrust are desired. Therefore consideration needs to be given to the possibility of feathering motion causing a flap and lead/lag response through mass and inertia effects. The blade is now constrained to feather through an angle 0 whilst the flapping and lagging angles are zero, see Fig. 4.6.

Now from Fig. 4.6:

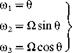
(4.16)

Fig. 4.6 Pure feather motion.

and:

ax = Q2eR ‘j

ay = О I (4.17)

az = О J

As before, substituting Equations (4.16) and (4.17) into Equation (4.9):

L = Ixx 0 + Ixx )2 sin 0 cos 0 M = Iyy )0 cos 0 — Iyy )0 cos 0 N =— (Ixx + Iyy) )0 sin 0 — (Ixx — Iyy) )0 sin 0 Hence:

L = Ixx0 + Ixx)20 "J

M = О і (4.18)

N =—2Ixx )0 0 J

The lagging moment due to feathering, 2Ixx)00, is usually extremely small when compared with the Coriolis flapping moment and can be neglected.

4.2 FLAP DYNAMICS

The above analysis and Equations (4.12), (4.15) and (4.18) show, to a first approxi­mation, that the only dynamic linkage between flap, lead/lag and feather is the Coriolis effect that causes a flapping blade to lead or lag. Thus in the absence of a S3 hinge,

lead/lag motion will not feedback to affect the flap response and it can be assumed that the feathering motion required to produce a flap response aerodynamically will not generate any dynamic effects that modify the flap behaviour. Consequently for the rotor the most fundamental dynamic equation is the flapping equation:

M.

Iyy p + )2(Iyy + mb Xg eR2 )p =-M or p + )2(1 + є)Р = Iа (4.19)

Iyy

To determine the nature of the flap dynamics it is necessary to consider the nature of the aerodynamic forcing. Three scenarios will be used to expose the basic dynamic characteristics of a typical rotor: a flap disturbance, the application of cyclic feathering and the application of a steady pitch/roll rate to the rotor. For simplicity all assume the helicopter is initially in a trimmed OGE hover.