Rotor flapping and disk tilt

Consider a helicopter hovering in still air. If the longitudinal airspeed of the helicopter is changed from zero, by a gust or pilot inaction, the disk will tilt upward over the nose if the airspeed change is positive, that is forward, and vice-versa. This phenomena, the ‘flap-back effect’, is very important in determining the static stability of the helicopter. Alternatively if the helicopter is allowed to sink the change in inflow will cause the rotor to generate more thrust thereby arresting the descent. In a similar manner a climb initiated by a gust will be damped out. Suppose a gust strikes the fuselage causing it to pitch up. This will have the initial effect of changing the pitch on the blades since the rotor will initially retain its position in space due to gyroscopic rigidity. Although the pilot has not applied any cyclic pitch a movement of the fuselage relative to the main rotor will have the same effect. Shortly after the fuselage pitches up the rotor will follow it and ultimately be re-aligned, at which point the lift will be equalized once again.

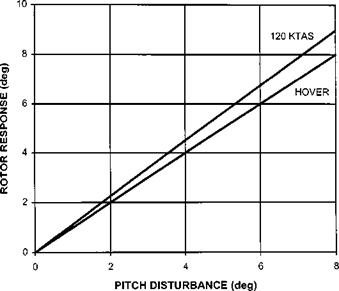
The response of the rotor to a change in forward airspeed, whilst in forward flight, is similar to that for the hover. The changes in lift on the advancing and retreating sides of the disk cause it to tilt up over the nose following an increase in airspeed and vice-versa (flap-back). The effects of changes in vertical speed and fuselage pitch attitude are different, however, with both situations giving rise to an unstable disk response. Suppose the helicopter develops a positive vertical speed (downwards). This will generate an increase in the angle of attack on both sides of the disk and hence an increase in lift. This increase is, however, not equal and the net result will be an upward tilt of the disk over the nose of the helicopter. The tilt back of the rotor will have the effect of increasing the AOA. If the action of a gust causes the helicopter to pitch nose-up this will increase the pitch of the advancing blade and reduce the pitch of the retreating blade as already described. The rotor will then flap in a ‘nose-up’ direction to achieve equality of lift, again as already mentioned. However due to the effect of the forward speed the attitude of the rotor relative to the fuselage at the point of lift equalization is further nose-up than the original disturbance. The tilt back angle required to equalize lift for a given pitch disturbance is determined in Table 4.8 and plotted in Fig. 4.19. For simplicity the rotor has a symmetric blade section and is initially at zero collective pitch (blade flapping is not considered). Note in this simple example that the blade pitch, measured relative to the horizon, is controlled solely by the swash plate tilt.

Table 4.8 Disk tilt response to a pitch disturbance (120 kts, rotor radius 6.5 m, RRPM 35 rad/s).

4.6.2 Main rotor contributions to speed and AOA stability

The foregoing discussion of the rotor response to changes in flight condition gives insight into the stability of a helicopter. Recalling that static stability is the initial response of the aircraft following a disturbance it is possible to lead from a considera­tion of speed and AOA stability to static stability. Before describing the stability of a conventional helicopter it will instructive to introduce the mechanisms by which control is effected. The basic method of control is through the generation of moments about the centre of gravity. In this case only pitching moments derived from the main rotor will be considered. On all helicopters a control moment is generated by changing the direction and magnitude of the thrust vector. Changes to the direction are achieved by disk tilt. An additional moment will arise on helicopters with a non-zero hinge offset, since as the disk tilts relative to the fuselage, centrifugal forces acting on the blades give rise to a couple which manifests itself as a hub moment which is proportional to the amount of disk tilt. Therefore, regardless of the type of rotor system, if a disk tilt is produced as a response to a disturbance a moment, pitching in this case, will be generated. Suppose the pilot trims the helicopter at a particular airspeed and then relaxes on the controls. Sometime later a gust strikes the aircraft causing the airspeed to increase. This increase will cause the rotor to flap-back, that is the disk will tilt rearwards. The movement of the disk relative to the fuselage will generate a nose-up pitching moment that will have the effect of reducing the airspeed. Therefore the main rotor generates a stabilizing contribution to the overall speed stability of the helicopter. Again suppose the pilot trims the helicopter, but this time the disturbance generates either a downwards component of airspeed or causes the fuselage to pitch upwards. In either case the result is an increase in the AOA on the advancing blade. Once again the rotor disk will tilt rearwards but this time further than the original AOA disturb­ance, thereby producing a net out-of-balance moment which generates a further disturbance. Therefore the main rotor generates a destabilizing contribution to the overall AOA stability of the helicopter.