Unsteady Reference Flight

Return to Eqs. (7.18) and (7.19), the general perturbation equations, and keep the unsteady term sflDIRDpDrlBrrI. They model the perturbations of aerospace vehicles in maneuvering flight. Unsteady means that the reference flight is rotating, like the pull-up maneuver of an aircraft, the circular intercept path of an air-to-air missile, or the pushdown trajectory of a cruise missile during terminal attack. If the parameters in the differential equations are functions of time, like the Mach dependence of aerodynamic coefficients, I call these terms nonautonomous.

Because we concentrate on nonspinning vehicles, the body frame is chosen as the dynamic frame, and we modify Eq. (7.18)

D’epb + sSlBIRBpBrplBr = efa + eft +(E – RBpBr)fgr (7.30)

and Eq. (7.19)

Dlelf + еПві RBpBrlBRr’ = єта + cm, (7.31)

To simplify these perturbation equations, second-order terms in є are neglected. Such terms will now be identified. First, the rotational time derivatives are trans­posed to frame Bp via the Euler transformation:

D1 spB = DBpspB + ПВрІєр’в

DlelBi = DBpslBJ + ГlBp, elBBl

then, Eq. (7.13) is used to replace ftBp!. Finally, substituting back into Eqs. (7.30) and (7.31) yields the second-order terms єПВІєрв and e£Ib’e:Ibr!. Neglecting these terms reduces Eqs. (7.30) and (7.31) to

DBpEp’R + RBpBrnRr, RBpBrEp’R + e£Ibi RBpBr pBr

= efa + ef, + (E – RBpBr)fgr (7.32) *

DRpeIbi + RBpBrnBrlRBpBrElBI + ESlBIRBpBrlBBr’ = Etna + єт, (7.33)

The second terms on the left-hand sides are the vestiges from the Euler transforma­tions. They couple the reference rotation £lBrI with the perturbations spB and e:Ibr .

We continue with the introduction of the linear velocity perturbation svB and the angular velocity perturbation єшВІ, using the definition of Eqs. (7.6) (mass does not change from the reference to the perturbed flight)

ep’B = e(mvlB) = emvg+mevg = meVg (7.34)

and Eq. (7.7)

ЄІВІ = Є(ІВШШ) = ЄІВШШ + IrEU>BI = ІдЄШВІ

We use the fact that the perturbation of the MOI tensor is also zero. This follows from the definition of the MOI perturbation Eq. (7.12), where the rotated MOI tensor IBrr, now coinciding with IRP, is subtracted from IBRp:

el = IBBpp – RBpBrIBrr RBpBr = 0

With the definition of Eq. (7.11) and replacing iBRr by IBBp, the angular momentum perturbations evolve with the definition of єшВІ [Eq. (7.9)] as follows:

eIbJ = 1ВрршВр1 – RBpBrl%uBrl = 1%{шВр1 – RBpBrcoBrI)

– lBpEU>BI

— 1Врєш

Substituting Eqs. (7.34) and (7.35) into Eqs. (7.32) and (7.33) produces the per­turbation equations of unsteady flight in tensor form suitable for applications

mDBpevB + mRBpB’TLBrIRBpBrsvIB + meSlBl RBpBrv’Br

= efa + ef, + (E – RBpBr)fgr (7.36)

I Bp DBpEOJBI + RBpBrnBrlRBpBrIBp)EOjm + ESlBIRBpBrIBBrru>Brl

= E, ma + Em, (7.37)

The perturbation variables are the linear velocity evb and angular velocity ешВІ. The perturbation attitude angles в, ф are contained in the small rotation tensor RBpBr. Look at the terms on the left-hand sides of both equations, going from left to right: first, the time derivative wrt the perturbed body frame in anticipation of using perturbed body coordinates; second, the unsteady term caused by the rotating reference flight. The last terms of the left sides have a different purpose in each equation. In the first equation it is the coupling term with the angular momentum equation through ешві. In the second equation this term makes an unsteady contribution of шВгІ, similar to the preceding term.

To use the equations in numerical calculations, we express them in body co­ordinates associated with the perturbed frame Bp. The rotation tensor [RBPBr]BP disappears, as we transform the reference variables [vBr]Bp, a>RrlRp, and |lB’rHp to the reference body axes ]Br. With the gravitational term expressed in inertial axes according to Eq. (7.25), Eqs. (7.36) and (7.37) become

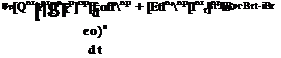BP + ,«[««’■’] ЙГК]ЙР + т[ЕиВІ}ВрШВг = [sfalBp + [ef,]Bp + ([T]BpBr – [EmfrlUgrV (7.38)

[sma]Bp + [Em,]Bp

We succeeded in expressing all perturbation and references variables in perturbed and reference coordinates, respectively. The transformation matrix [T]BpBr consists of the attitude perturbations в, ф, whereas [T]BrI establishes the coordinates of the gravitational force in reference body axes. Frequently, you will choose the Earth as inertial frame and the associated local-level coordinate system (see Sec. 3.2.2.7). Then, the gravitational force will take a particular simple form [/gr]L = m[0 0 g]. How can we apply these equations? Imagine an air-to-air engagement. The target aircraft pulls a high-g maneuver, and the missile goes for the kill in a circular trajectory. Both execute unsteady circular trajectories. Record the reference values of [vBr]Br, a)Rr,R’ and [T]BrI for the aircraft and the missile. To analyze the dynamics of either vehicle, insert these reference values into Eqs. (7.38) and (7.39) and provide the appropriate mass and aerodynamic and propulsive parameters.

Equations (7.38) and (7.39) are the starting point for the two examples of Sec. 7.5. But before these equations can be derived, we have to deal with the subject of aerodynamic modeling and linearization.