Airspeed

Determining the airspeed of an aircraft involves finding the difference between total, stagnation or pitot pressure and static pressure. When a helicopter moves through the atmosphere air entering the pitot probe will be brought to rest thus the pressure sensed by this probe will be its stagnation or pitot value. If the static pressure is subtracted from this pitot pressure (Pp) then the remaining dynamic pressure will be a function of the speed of flight. Thus true airspeed (V), which is a function of this dynamic pressure, is not measured directly but inferred by the action of the pitot – static system.

How the indicated airspeed (Vi), that is the velocity information presented on a typical airspeed indicator (ASI), relates to the free-stream velocity or true airspeed (V) must now be considered. Air is a compressible fluid whose characteristics can be expressed in the form of the compressible Bernoulli equation which can be manipu­lated to give a relationship between stagnation pressure, static pressure (assumed to equal the ambient pressure) and true Mach number:

This equation can be further modified to yield the pressure difference sensed by the ASI. Thus:

1 + PP – P

2

M 2 =

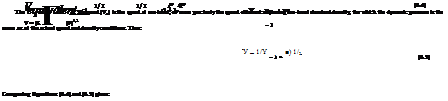Since M = Vla and a, the local speed of sound, equals —yP/p, then:

V=

It is standard practice, however, to calibrate airspeed indicators at sea-level. This is achieved by assuming a sea-level standard pressure (P0 = 101 325 N/m2) in the calibration. Thus the calibrated airspeed (Vc) is given by:

The difference between the calibrated airspeed and the equivalent airspeed is called the scale altitude correction (*Vc), thus:

V1

V = = -r(Vc + *Vc) (6.6)

The size of this scale altitude correction depends on the Mach number and altitude of flight. Since most rotorcraft operations take place below 10000 ft (3000 m) and 200 kts it would be useful to determine whether a scale altitude correction need be applied during rotary wing flight data processing. At 10000 ft the International Standard Atmosphere gives a static pressure of 69 671 N/m2 and a temperature of

267.3 K. A true airspeed of 200 kts results in a Mach number of 0.313 and gives a dynamic pressure of 4903 N/m2. Thus the equivalent airspeed is 171.9 kts and the calibrated airspeed is 172.5 kts. So even for high-altitude high-speed helicopters the scale altitude correction is less than 0.4% and is therefore usually ignored. Thus Equation (6.6) becomes:

VV

V e ________ ‘ c

—CT —CT

A distinction now has to be made between the local static pressure (P„) of the air through which the rotorcraft is flying and the pressure (Ps) measured via the static vents located on the aircraft skin. Equally if the pitot pressure is measured incorrectly, as a result of sideslip for example, there will be a difference between the true total or

pitot pressure (Pp) and that recorded by the pitot probe (Pp). As a result of these potential error sources, the indicated airspeed, Vi, is given by: