Basic Concept

Suppose a damping term, D(x), is added to the right side of the momentum equation of the linearized Euler equations in dimensional form as follows:

d u 1 d p

—— 1—– –

dt p0 дX

Let the spatial derivative be approximated by the 7-point stencil DRP scheme. The discretized form of Eq. (7.10) is

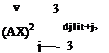It will now be assumed that De is proportional to the values of ut within the stencil. Let dj be the weight coefficients. Eq. (7.11) may be written as

where v is the artificial kinematic viscosity. v/(Ax)2 [4] has the dimension of (time)-1, so that dj’s are pure numbers. Now djs are to be chosen so that the artificial damping would be effective mainly for high wave number or short waves.

The Fourier transform of the generalized form of Eq. (7.12) is,

di v,

d + ”’ = "<Arf2D (aAx)u (7-13)

where

3

D (aAx) =Y^ djeijaAx j=-3

V (Ax)[5]

On ignoring the terms not shown in Eq. (7.13), the solution is,

Since D (a Ax) depends on the wave number, the damping will vary with wave number. It is desirable for D to be zero, or small for small a Ax, but large for large a Ax. This can be done by choosing dj’s appropriately. But one must be careful to make sure that the damping term would not cause undamping or numerical instability. The purposes of the following three conditions that are to be imposed on D are self-evident.

1. D (a Ax) should be a positive even function of a Ax. The even function condition is ensured by setting dj = dj. Thus,

3

D (a Ax) = d0 + 2 ^2 dj cos( j a Ax). (7.16)

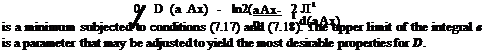
j=-3

For example, the coefficients of a very useful damping curve for problems involving discontinuous solution are (a = 0.3п, в = 0.65n) as follows

d0 = 0.3217949913 dx = d_! = -0.2328759104 d2 = d_2 = 0.08910250435 d3 = d_3 = -0.01712408960

A plot of D versus a Ax for this choice is shown in Figure 7.2.