Complex Numbers
To have an understanding about the complex numbers will be of great value to deal with the Joukowski transformation, to be taken up in Chapter 4. Let us briefly discuss the essential aspects of complex numbers in this section.
A complex number may be defined as a number consisting of a sum of real and imaginary parts. Let x and y be the real numbers; positive or negative. Let i be a symbol which obeys the ordinary laws of algebra, and also satisfies the relation:
i2 = -1. (3.5)
The combination of x and y in the following form:
z = x + iy (3.6)
is then called a complex number.
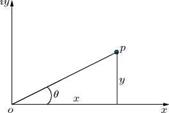
A complex number z can be represented by a point p whose Cartesian coordinates are (x, y), as shown in Figure 3.6.
The picture, such as Figure 3.6, in which the complex number is represented by a point is called the Argand diagram. In this representation the complex number z represents the point p or (x, y).
|
Figure 3.6 Representation of a complex number in xy-plane. |
The numbers x and y in Equation (3.6) are called the real and imaginary parts of the complex number z, that is:
|
x = Real part of z, y = Imaginary part of z. |
|
|
When y = 0 the complex number z is said to be purely real and when x = 0 the complex number z is said to be purely imaginary. Two complex numbers which differ from the sign of i are said to be conjugates. Usually a conjugate number is represented with an “overline.” For example: |
|
|
z = x + iy |
(3.7a) |
|
z = x — iy. |
(3.7b) |
|
The simple fact that: |
z + z = 2x z — z = 2iy
imply the following two simple but important theorems:
Theorem 1: The real part of the difference of two conjugate complex numbers is zero.
Theorem 2: The imaginary part of the sum of two conjugate complex numbers is zero.
The point p which represents a complex number in the xy-plane can also be described by polar coordinates (r, в), in which r is necessarily positive. By Euler’s theorem, we have:
cos в + i sin в = еів.
Therefore:
z = x + iy = r cos в + ir sin в
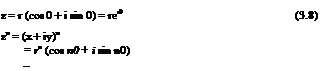 |
Note that:
2 cos 0 = ei0 + e-i0 2i sin 0 = ei0 — e-i0.
When polar coordinates are used the positive number r is called the modulus of z, expressed as:
r = mod z = |z|
= J x2 + y2
= s/zz.
Then the product of two conjugate complex numbers is the square of the modulus of either.
The angle 0 is called the argument of z, expressed as:
0 = arg z.
Therefore, all complex numbers whose moduli are the same and whose arguments differ by an integer multiple of 2n are represented by the same part in the Argand diagram. The value of arg z (that is, angle 0) that lies between — n and +n is the principal value. The principal value of the argument of a positive real number is zero, and the argument of a negative real number is n.
 |
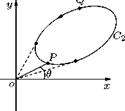 |
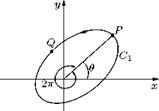
Let us consider a curve C encircling the origin and curve C2 which does not encircle the origin, as shown in Figure 3.7. If 0 is the initial value of the arg z and if z is represented by the point P, it is clear that when a point Q originally coinciding with P is moved round Q in the clockwise direction, the corresponding value of its argument increases, and when we finally return to P after going one round, we have the arg z = 0 + 2n. On the other hand, if we go round C2, the argument of Q decreases at first until OQ becomes a tangent to C2, then increases until OQ again becomes a tangent and finally decreases to the initial value. Thus if arg z has a given value at one point of a curve such as C2 which does not encircle the origin, the value to the argument of z is one-valued at every point inside and on C2, provided when the arg z is assumed to vary continuously with z.
Figure 3.7 Two curves in the xy-plane.
 |
Example 3.1
A particle moves in the xy-plane such that its position (x, y) as a function of time t is given by:
i + 2t z = T.
ti
Find the velocity and acceleration of the particle in terms of t.
3.4 Summary
The transformation technique which transforms an orthogonal geometric pattern, composed of elements of certain shape, into an entirely different pattern, whilst the elements retain their form and proportion is termed conformal transformation.
In the z-plane (physical plane) point p is located by z = x + iy, and in the f-plane (transformed plane), the corresponding point P is located by f = § + in. The relation between z and f is a particular specified function of f, in terms of z. That is:
This function is known as the transformation function. In the transformation, both the elements of the crossing arc segments are rotated through the same angle. Therefore, the angle of intersection must remain unchanged during the transformation.
The transformation function is essentially of the vector type:
f = f (z),
where z = x + iy and f = § + in.
A general form of the transformation function is:
where A0, A1, etc. and B1, B2, etc. are constants and vectors or combinations of constants and vectors, respectively.
The length ratio of corresponding elements in the z- and f-planes is given by:
![]() f ‘(z)
f ‘(z)
![]()
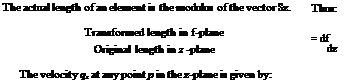 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()