Flat-Earth Equations of Motion

Unless you work exclusively with space applications, you will encounter the flat-Earth equations of motion more often in six-DoF simulations. We first derive the general form of the equations of motion and then specialize them for missiles
and aircraft based on the characteristic of the MOI tensor. Spinning missiles and Magnus rotors will each require a fresh approach.

Let us first derive the translational equations of a flight vehicle subjected to the aerodynamic and thrust forces fa and the gravitational acceleration g. Newton’s second law wrt the inertial frame I states that the time rate of change of linear momentum equals the externally applied forces:

= f a p + mg

where m is the vehicle mass and vB is the velocity of the missile c. m. В wrt the inertial reference frame I. The flat-Earth assumption allows us to declare the Earth frame E as the inertial frame. Therefore, Newton’s law becomes

mDEvEB = fa’P+mg

To model the aerodynamic forces, we need access to the incidence angles. They are calculated from the velocity vector as perceived from the vehicle as reference frame. Its time rate of change DBvf is therefore referred to the vehicle B. This desired shift of reference frame is accomplished through the Euler transformation

mDBvB + mflBEvB = fa p + mg (10.1)

These are the translational equations of a vehicle over a flat Earth. The second term on the left-hand side is identified as the tangential acceleration term. The equation is valid in any coordinate system.

Now comes the important event of picking the coordinate system. Actually, I have already preempted the decision by transforming the rotational derivative to the body frame. To generate the ordinary time derivative, the rotational derivative must be expressed in the coordinate system ]B associated with the frame B. Expressing all terms in ]B yields

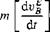+ m[QBE]B[vE]B = [fa, p]B+m[g]B

This selection suits us well because it models [vB]B, the linear velocity of vehicle wrt Earth, as needed for incidence angle calculations; [Q. BE]B, the angular veloc­ity of vehicle wrt Earth; and [fa, P]B, the aerodynamic and propulsive forces, all expressed in the preferred coordinate system ]B. Only the last term is better for­mulated in the local-level coordinate system ]L so that g takes on the simple form [g]L = [0 0 g], Alas, the direction cosine matrix [T]BL appears, which we will derive later from Euler’s equations. The translational equations in matrix form, suitable for programming, are then

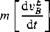+ m[0.BE]B[ vE]B = [fa, p]B + m[T]BL[g]L (10.2)

Much labor is involved in modeling the forces [fa, p]B. In the next section I will give you a taste for the complexity of six-DoF aerodynamics, both for missiles and aircraft. Here we proceed blissfully and code the equations directly with program languages like FORTRAN or C. You can also choose the simulation environment

CADAC, which provides the utility subroutines that enable vector state variable integration and matrix manipulations. Written out in coordinate form, we get

	•	du/dt	В	0	—r	4	В	u	в’
m ■		dv/dt	+	r	0	-P		V
		dw/dt		~q	P	0		w

	г 1	В			-i	BL	– -■
	fa, pi			t2	*13		0
=	fa, pi	+	hi	t22	*23		0
	fa, pi		hi	*32	*33		mg

fa, Pi m

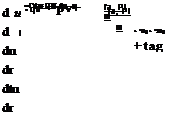These equations are simple enough to be expressed in scalar form:

The integration of these differential equations yields the velocity vector that must be integrated once more to obtain the location of the missile c. m. В wrt an Earth reference point E

[Ле] = [uf] (10.4)

The integration is best carried out in the local-level coordinate system. Therefore, given [uf ]B, we program the second set of differential equations as

and in coordinate form

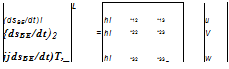(10.6)

Here we have the six first-order differential equations that govern the transla­tional motions of a vehicle with the Earth as the inertial reference frame. Equa­tions (10.3) are nonlinear and coupled by the body rates p, q, and r and the direction cosine matrix [T]BL with the attitude equations. The nonlinearity enters through the incidence angles in the aerodynamic force and moment calculations [for instance, seeEqs. (10.61) and (10.62)]. Equations (10.6) are linear differential equations, again coupled by [T]BL with the attitude equations.

The rotational degrees of freedom are governed by Euler’s law that states that the time rate of change of angular momentum equals the externally applied moments.

To conform to the translational equations, we pick E as the inertial frame:

DElBE = mB (10.7)

where lBBE = ІвшВЕ is the angular momentum of body В wrt frame E referred to the c. m. B, IBB is the MOI of missile body В referred to the c. m., and mB the aerodynamic and thrust moments referred to the c. m.

Just as in the case of the translational equations, we take the perspective of the vehicle body frame В and use therefore the Euler’s transformation to transfer the rotational derivative to the body frame

DBlf + ПВЕ1ВВЕ = mB

Let us focus on the rotational derivative, expanding the angular momentum vector, and applying the chain rule

DBlBBE = Db(Ibbube) = DbIbbube + 1BBDB шВЕ = IbDbujbe

For a rigid body DBIB is zero, a simplification that motivates the transformation to the body frame. The equation reduces to

IbDbube + ПВЕІвиВЕ = mB (10.8)

These are the rotational equations of a vehicle with respect to a flat Earth. The second term on the left-hand side is the apparent gyroscopic effect, arising from the choice of the body as reference frame.

As a coordinate system, we pick again the body coordinates because they express the MOI tensor in constant form, yield the ordinary time derivative of the body rates, and express the aerodynamic moments in their preferred form:

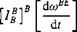+ [Qbe]b[Ib]B[wbe]b = [mB]B (10.9)

For an arbitrary [IB]B we premultiply the equation by its inverse and solve for the time derivative

B = {[Ibb}B)–[Q. be]b[Ib]BWbe}b + [mB]B) (10.10)

These three first-order nonlinear differential equations couple with the translational equations (10.2) only through the aerodynamic moments [mB]B. The form of the MOI tensor [IB]B establishes a major demarcation. Missiles exhibit pure diagonal forms, resulting in simple equations, whereas aircraft have one off-diagonal ele­ment that leads to more complex solutions. We reserve therefore in the following sections different treatments for missiles and aircraft. Here we complete that part of the treatment of the attitude kinematics, which is common to both.

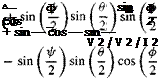
Given the body rates [coBE]B = [p q /’] from Eq. (10.10), a second set of differ­ential equations provides the body attitudes. We discussed the three possibilities in Chapter 4: Euler angle, quaternion, or direction cosine equations. Here we pursue the quaternion approach. Go back to Sec. 4.3.3 and review quaternions, or, like many other impatient engineers, just program the following equations.

The four-quaternion elements qa, qi, qi, and q- are related to the three body-rate components by four linear differential equations:

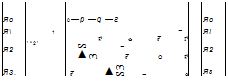(10.11)

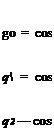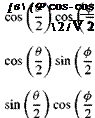To solve the equations, they must be initialized. Unfortunately, quaternions are hard to visualize; therefore, it is more likely that the initial Euler angles are given. The conversions are

For example, an aircraft’s Euler angles are zero if it starts flying north, straight, and level. Its quaternions are also zero with the exception of the scalar component Яо = 1.

If the differential equations (10.11) could be solved exactly, we would not have to worry about maintaining the orthonormality of the quaternion. However, the use of numerical integration schemes introduces errors caused by finite word length and discretization of time. We can maintain the unit norm of the quaternion by a proven trick.1 Let the orthonormality error X be

* = 1 – (Яо + V? + ЯІ + Яз)

and add to the right side of Eq. (10.11) the factor kX{q}, where {q} is the four – element quaternion vector. The constant к is chosen such that к At < 1, with At the integration interval. Its value is not crucial. I have tried several к and found the effect quite acceptable. For the CADAC SRAAM6 simulation, after some testing I picked к = 0.5 at At = 0.001.

Given the quaternions, the Euler angles are derived from the following relation­ships:

The first equation has singularities at [r = ±90 deg, and the last equation at ф = ±90 deg. These singularities are not serious because they occur during off-line calculations and not inside the differential equations. They can easily be bypassed by programming around them.

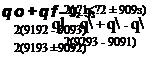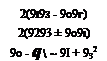The direction cosine matrix [T]BL could be calculated from the Euler angles. However, because of the singularities, it is better to use the quaternion relationship directly:

(10.14)

In summary, the three translational degrees of freedom are governed by the six first-order differential equations (10.2) and (10.6). The three rotational degrees of freedom are calculated from the three first-order differential equations (10.10) and the four kinematic differential equations (10.11).

With the general equations of motion of a vehicle over a flat Earth in place, we now turn to special expressions of Eq. (10.10). The form of the MOI tensor will determine whether we call them missile or aircraft equations.