Magnus rotor

10.1.1.4 If you liked the derivation of the spinning missile equations, you will really enjoy this excursion into the dynamics of bodies that spin about a horizontal axis. They are my favorite subject because I spent five years studying their characteristics, culminating in my dissertation.2

Spinning bodies were first investigated by Heinrich Gustav Magnus in 1852. He demonstrated experimentally that a body rotating in an airstream experiences a force that acts substantially normal to the airflow. An autorotating flight vehicle, designed to develop this Magnus force efficiently and to employ it as the major lift force in free flight, is called a Magnus rotor. It consists of a center body with driving vanes and endplates.

Figure 10.3 depicts a Magnus rotor spinning about a near horizontal axis and gliding with the velocity vf. The spin axes 2s and the velocity vector form a plane containing the roll axis Is normal to the spin axis. The yaw axis 3L is parallel to the gravitational acceleration.

The dynamics of Magnus rotors can best be explained in terms of a horizontally spinning gyroscope that is subjected to aerodynamic forces. The dynamic motions of the glide trajectory are rolling <j>, yawing ф, and sideslipping /8. They exhibit three modes: nutation, precession, and undulation. The nutation and precession
modes are those of a gyroscope with the modification that the nutation is aerody – namically dampened. New is the undulation mode. It arises from the interaction of aerodynamic moments—generated by /3—and gyroscopic precession. In general, this mode can be oscillatory or aperiodic.

You can understand the fun I had working on this project, developing the theory, building the computer simulation, and flight testing some specimens. For our current purpose we limit the discussion to the derivation of the equations of motion, the starting point of any six-DoF simulation of Magnus rotors.

As always, the translational equation is based on Newton’s second law

mDEv I = fa + fg

and the attitude equation derives from Euler’s law

DElf = mB

with aerodynamic forces and moments fa, mв and the gravitational force fg = mg.

Just as I used a nonspinning frame B’ for the spinning missile, in the same vein I introduce here a frame that is attached to the Magnus rotor but does not follow its spin. It is called the stability frame and is defined by the spin axis and the projection of the velocity vector on the symmetry plane of the rotor. The associated stability coordinate system has its 2s axis aligned and in the direction of the spin vector, its Is axes parallel and in the direction of the projection of the velocity vector on the symmetry plane. The third axis 3s completes the triad. The transformation matrix [T]5L of the stability wrt the local-level axes follows the conventional transformation of Euler angles: yaw j/sL, pitch 6sl. and roll ф%і (see Sec. 3.2.2.4).

The first step is to transform Newton’s equation to the stability frame and express the terms in stability coordinates

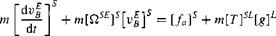
(10.25)

Focus on the meaning of [f25£]s. It is the skew-symmetric form of the angular velocity vector of the stability frame wrt Earth, which embodies the rolling and yawing rates, but excludes the spinning motion. The choice of the stability coor­dinates is dictated by the method of the aerodynamic force measurement. In the wind tunnel the sting supporting the model is centered at the spin axis, allowing the Magnus rotor to rotate freely. The force measurements, taken by the sting, are in stability axes. By the way, the term stability axes is borrowed from airplane dy­namics. There and here, the I s axis is also defined as the projection of the velocity vector on the symmetry plane of the aircraft.

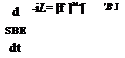From the velocity vector [uf ]s and the transformation matrix T]SL. we can get by integration the position of the Magnus rotor [_sbel, i. e., the displacement of the c. m. В with respect to an Earth reference point E, expressed in local-level coordinates.

Equations (10.25) and (10.26) are the translational equations of Magnus rotors. The angular velocity [f2S£]fl and the transformation matrix [ 7" ] s/ are still to be supplied by the rotational equations.

Similar to spinning missiles, the more exciting part is the derivation of the attitude equation. Applying Euler’s law and transforming the rotational derivative to the stability frame, we obtain

Dslf + nSElf – =mB

We divide the angular velocity шВЕ of the missile body В wrt the reference frame E into two parts:

, ,BE __ ,BS I . ,SE

UJ = LO — UJ

The first part is the spin rate, and the second one is the angular velocity of the nonspinning stability frame wrt Earth. Similarly, the angular momentum is split into two parts

If = IBBUJBE = IBBuBS + 1bujse (10.28)

We form the rotational derivative as required by Eq. (10.27)

Dslf = Ds(lBB u>BS) + Ds(Ibujse)

= IBBDsuBS + IbbDsuse (10.29)

where we made use of DSIB = 0 because the Magnus rotor’s MOI about the spin axis is independent of spin attitude. This simplifying assumption is true at least approximately because the effect of the driving vanes is insignificant. Substituting Eqs. (10.28) and (10.29) into Eq. (10.27) yields the atitude equation of motion

IbDsujbs + IbbDsuse + nSEIBuBS + tlSEIBBuSE = mB (10.30)

The total rate of change of angular momentum consists of the spin contribution— first term—and the stability frame rotations—second term. The primary gyroscopic coupling stems from the third term, which dominates the fourth term.

Just as the stability coordinates were used for the translational equations, they are also best suited for the attitude equation. The aerodynamic moment [mj]s is given in that form, the angular velocity [ws£]s is needed by the translational equations, and the rotational time derivatives become the ordinary derivatives. For these reasons we express the rotational equations in stability coordinates

+ inSE]S[lS]S([‘Js]s+ [**]*) = [mB]s

(10.31)

Another important fact is that the MOI tensor is constant in stability coordinates and has a particularly simple diagonal form (note because of symmetry /3 = /j)

~h о o"	5	V	5	p’
О О	, [wBSf =	CO	, [«S£]S =	я’
0 0/!		_0		r’

with the angular velocities also included. Substituting the matrices into Eq. (10.31) yields

0	s	~Wp’/dt)~	s	0	—r’	я’	S	~h	0	o"
I2(dco/dt)	+	hW/dt)	+	r’	0	-P’		0	h	0
0		_/!(drVdO_		-Q’	P’	0		0	0	h_

	/	"o’	s	/	s		p -1
		P		mBl
X		CO	+	Я’		—	тВг
		_0		r’	)		твъ_

and the three scalar equations

h ( – hcor’ – q’rh ~ Л) = mBl

r(do> d q’

/2U+^J=W52

h ( J + htop’ + p’q’ih ~ h) = mB,

Although the pitch rate of the stability frame is not zero—magnitude of the un­dulating flight-path rate, it is much smaller than the spin rate, and therefore the terms containing q’ can be neglected. With this simplification and solving for the

derivatives yields the simple attitude equations of Magnus rotors:

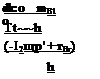dp’ _ (hcor1 + mBl) dt I

The first and last equations govern the gyroscopic coupling, which is a function of the spin MOI ratio h/h, the spin rate со, and the angular coupling rates r’ and p’. A positive yaw rate r’ induces a positive change in roll rate p’. whereas the roll rate has the opposite effect on the yaw rate. This purely gyroscopic behavior is modified by the aerodynamic moments mBl and m B}. The second equation simply describes the spin history. In a typical flight the Magnus rotor will reach a steady-state spin rate, indicating that the torque of the driving vanes equals the skin friction on the cylinder and the endplates.

To build a complete six-DoF simulation of Magnus rotors, you would have to program Eqs. (10.25), (10.26), and(10.32), supplemented by quaternion equations for the calculation of the transformation matrix [r]SL. Figure 10.2, with the proper substitutions for Newton’s and Euler’s equations, can serve as a blueprint.

You may have noticed already the great similarity between the equations of a spinning missile and a Magnus rotor. Both use a nonspinning frame that slips over the body, which we called either the nonspinning body frame B’ or the sta­bility frame S. Associated with the frames are the nonspinning body or stability coordinate systems. They serve as the axes for recording the aerodynamic forces and moments in wind tunnels. The gyroscopic coupling is evident in both cases and gives rise to nutation about the velocity vector of the missile and normal to the velocity vector for the Magnus rotor. In either case the development of a full six-DoF simulation would follow the same pattern.

The four models of missile, aircraft, spinning missile, and Magnus rotor cover every conceivable aerospace vehicle that you may have to simulate. You can pro­gram them in matrix form or, in some simple instances, as scalar equations. If guidance and control systems are part of the vehicle, you will have to supplement your simulation with the appropriate code.

One simplification is common to all: the equations of motion were derived with the Earth as inertial reference frame and its curvature unfurled into a flat surface. This assumption is acceptable as long as the vehicle travels at moderate speeds (less than Mach 5) and at low altitudes (less than 30 km). At higher speeds and altitudes, we have to abandon the flat-Earth assumption and consider Earth as a spheroid moving with respect to the sun’s ecliptic.