Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Numerical Example
To illustrate the effectiveness of artificial selective damping, consider again the simple wave problem with discontinuous initial condition. On incorporating artificial selective damping to the DRP scheme, the finite difference equations are
3
Ul = T ^ ^ bjEt
j=0
3
рГГ) = pf + At Ь^П_j)
 |
 |
 |
j=0
 |
 |
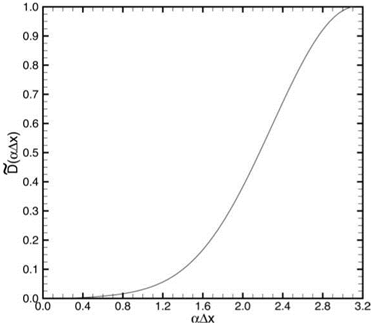
where Ra = a0kx/v is the artificial mesh Reynolds number. In the numerical simulation below Ra1 is given the value of 0.3.
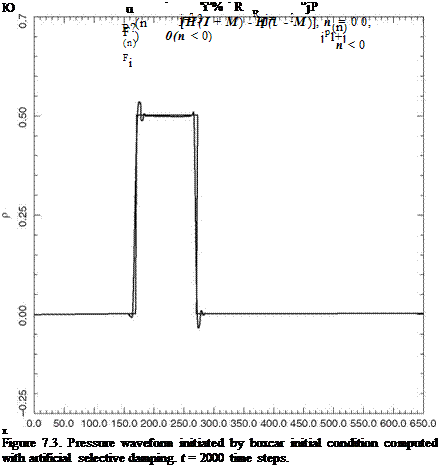
In the course of computing the numerical solution of Eq. (7.19), it is noticed that the short waves corresponding to grid-to-grid oscillations that are subjected to most intense damping are damped out almost immediately after they are generated. The damping for the spurious waves with longer wavelengths is smaller. Their presence in the numerical solution can still be seen after 200 time steps. At t = 500At, they, too, are almost completely eliminated. Figure 7.3 shows the calculated pressure waveform at t = 2000At. Essentially all the spurious waves, except for two spikes, have been damped out. The computed solution is now a reasonably good approximation of the exact boxcar solution. Of course, the finite difference solution is not perfect. It does not faithfully reproduce the sharp discontinuities. Each discontinuity is spread over
a distance of about 5 to 6 mesh spacings. This is closed to the minimum wavelength that the scheme can resolve.